|
It is important to remember that the natural logarithm function, ln(x),
and the natural exponential function, ex, are inverse functions.
When a function is composed with its inverse, the starting value is returned.
ln(ex) = x and eln(x) = x
When studying ex, some people find it easier to express ex, as exp(x),
so that the composition of functions is more
clearly observed.
ln(exp(x)) = x and exp(ln(x)) = x

Examples:
| |
Simplify: |
Answer |
1. |
ln(ex) |
Knowing that ln(x) and ex are inverse functions, the simplification under composition is x.
ln(ex) = ln(exp(x)) = x |
2. |
ln(e) |
Noting that the exponent on e is 1 (the x-value is 1), and applying what we just saw in #1, we know the simplification is one.
ln(e) = ln(exp(1)) = 1 |
3. |
eln(x) |
Again, we know that ln(x) and ex are inverse functions, so the simplification under composition is x.
eln(x) = exp(ln(x)) = x |
4. |
eln(7) |
Noting that the x-value is 7,exponent on e is 1, and applying what we just saw in #3, we know the simplification is seven.
eln(7) = exp(ln(7)) = 7 |
5. |
e3ln(4) |
 That "3" is interfering with the composition of the inverse functions. Move the "3" by using the log property that That "3" is interfering with the composition of the inverse functions. Move the "3" by using the log property that
ln ar = r ln a.
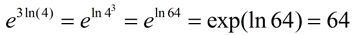
|
|
For help with exponential expressions on your calculator, click here.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
|
|