|
Directions: Read carefully. Show your work.
1. |
Riley, an abandoned cat, was found and taken to a local animal shelter. If untreated, the number of fleas on Riley, when he arrived at the shelter, would have started multiplying weekly according to the equation f (x) = 6(2)x. The number of weeks since arriving at the shelter is x and the number of fleas is f (x). |
|
| |
a) How many fleas were on Riley when he arrived at the shelter?
Choose:
|
b) How many fleas would have been on Riley 6 weeks after arriving at the shelter if he was not treated?
Choose:
|
c) At what rate are the number of fleas increasing each week?
Choose:
|
|
2. |
The table below shows the exponential decline in employment for a corporate business over time where t is the number of years since 2012.
time in yrs. |
0 |
1 |
2 |
3 |
workers |
8000 |
7600 |
7220 |
6859 |
|
|
| |
a) What was the initial number of employees when this study began?
Choose:
|
b) What is the rate of decay?
Choose:
|
c) What is the decay factor?
Choose:
|
d) Which exponential decay function models this business?
Choose:
|
|
3. |
The number of cell phones being used worldwide grew from 500 million in 2000 to 6,880 million in 2013.
a) Find the annual growth rate of cell phone usage.
b) Write an exponential equation to model this use of cell phones in terms of years.
c) Predict the number of cell phones in use in 2016 based upon your equation.
|
|
|
4. |
After mixing Jello, it is placed in the refrigerator to cool, where the constant temperature is 36º F. When placed in the refrigerator, the temperature of the Jello was 85º F. According to Newton's Law of Cooling, the temperature of the Jello can be modeled by: |

|
| |
T(t) = 36 + (85 - 36)e-kt
where t = time taken for the cooling
T(t) = temperature of the Jello at time t
k = decay constant
a) If the temperature of the Jello after 20 minutes is 60º F., find the decay constant.
b) How long will it take for the Jello in the refrigerator to reach a temperature of 40º F. ? (Round to nearest minute.)
|
|
5. |
Archaeologists use carbon-14 dating to determine when very old organisms died. All living organisms contain carbon, which is continually replenished through food and air. Carbon-14 decays over time into carbon-12. When an organism dies, this decay continues, disrupting the normal ratio between carbon-14 and carbon-12. |
| |
Dr. Jones has discovered a mummy which contains only 35% of its original carbon-14. Knowing the half-life of carbon-14 to be 5730 years, how many years have passed since the death of the mummy?
|
 |
|
6. |
The Savannah habitat that sustains African lions has shrunk by 75% in the past half-century. As a result, the population of lions has decreased from 100,000 (50 years ago) to 32,000 today.
|
|
| |
Using an exponential function, such as
f (x) = abx, represent this decline in the lion population.
|
|
7. |
Radioactive iodine is used in the treatment of thyroid problems. Its half-life is 8 days.
a) If an initial dosage, A, is given to a patient, find the decay rate.
b) Write a formula for the amount of radioactive iodine in the blood as a function of time in days.
c) Find the percentage of radioactive iodine remaining in the blood after 10 days.
|
|
|
8. |
The number of wolves in the wild in the northern section of a county is decreasing at the rate of 3.5% per year. An environmental group counted 80 wolves in the area. After how many years will this population of 80 wolves drop below 15 wolves, if this rate of decrease continues?
|
|
|
9. |
A dead body is found in an office building at 10 a.m. At that time, the coroner measured the body temperature to be 85.6º F. A second reading measured at noon found the body temperature to be 82.6º F. Assume room temperature to be a constant 70º F.
The coroner uses a formula derived from Newton's Law of Cooling, a general cooling principle, to calculate the elapsed time since a person has died. The formula is:
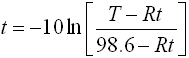 where T = the body's measured temperature Fº
where T = the body's measured temperature Fº
Rt = the constant room temperature
t = the elapsed time in hours since death. |
The most accurate estimate of the time of death is found by taking two readings and averaging the two calculated times of death.
According to the coroner, what would be the estimated time of death to the nearest minute?
|
|
10. |
We are actually living near the bottom of an ocean of air. At sea level, the weight of the air presses on us with a pressure of approximately 14.7 lbs/in2. At higher altitudes, less air means less weight and less pressure. Pressure and density of air decreases with increasing elevation.
The formula at the right shows that atmospheric pressure decays exponentially from its value at the surface of the body where the height, h, is equal to 0. When h0 = h, the pressure has decreased to a value of e-1 times its value at the surface.
|
Determining Atmospheric Pressure
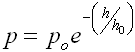
p = atmospheric pressure
(measured in bars)
h = height (altitude)
p0 = pressure at height h = 0
(surface pressure)
h0 = scale height
|
The surface pressure on Earth is approximately 1 bar, and the scale height of the atmosphere is approximately 7 kilometers.
Earth: p0 = 1; h0 = 7 |
|
|
a) Estimate the pressure at an altitude of 3 kilometers in Earth's atmosphere.
b) Estimate the pressure of an altitude equivalent to the height of Mount Everest (the highest point on Earth). The altitude of Mount Everest is 8,848 meters. (Change meters to kilometers.)
c) Estimate the pressure of an altitude equivalent to the height of Mount Kilimanjaro, 5,895 meters.
d) Estimate the pressure in the Earth's stratosphere at a height of 35 kilometers. This pressure will be approximately equivalent to the pressure on Mars.
e) Using your findings from parts a, b, c and d, prepare a scatter plot of the altitude in kilometers and the air pressure in bars. Find an exponential model equation for this data.
|
|
11. |
Drugs break down in the human body at different continuous rates of decay. Tylenol (acetaminophen) metabolizes and is eliminated at the rate of approximately 24% per hour. Advil (ibuprofen) metabolizes and is eliminated at the rate of approximately 29% per hour. Under a Doctor's care, Patient N is given 800 mg. of Tylenol, and Patient M is given 1000 mg. of Advil.
a) Using the function A(t) = A0e-kt for the breakdown of the drug, write a function for each of the patients N(t) and M(t), to represent the breakdown of the respective drugs. |
A(t) = A0e-kt
A(t) = amount left in body
A0 = initial dose
k = decay rate
t = time in hours |
|
b) Graph each of the functions.
c) To the nearest hour, t, when does the amount of the drug remaining in patient N begin to exceed the amount of the drug remaining in patient M ?
d) Patient N asks the doctor for another dose of Tylenol. The doctor agrees to allow patient N to take another 800 mg. dose once there is only 5% of the original dose remaining in the body. How long will patient N have to wait (to the nearest tenth of an hour), before taking another dose of this extra-strength Tylenol?
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|