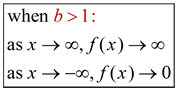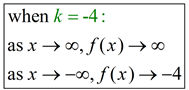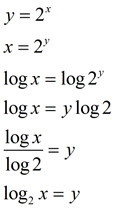|
The exponential function with base b is defined by
y = bx
where b > 0, b≠ 1, and b is a constant.
The independent variable is x with the domain of real numbers.
|
|
Let's examine the function: 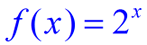
The value of b (the 2) may be referred to as the common factor or "multiplier". It may also be referred to as the "ratio" of successive terms. Remember, exponential functions grow by common factors over equal intervals.
|
x |
f (x) = y |
-2 |
2-2 = ¼ |
-1 |
2-1 = ½ |
0 |
20 = 1 |
1 |
21 = 2 |
2 |
22 = 4 |
3 |
23 = 8 |
|
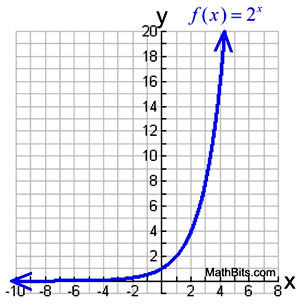 |
Most exponential graphs resemble this same basic shape. Notice that the y-values of the graph are very, very small on its left side making it extremely close to the x-axis. As the x-values increase to the right, the graph's y-values grow faster and faster, shooting quickly off the top of the graph.
Note: In a linear graph, the "rate of change" remains the same across the entire graph.
In an exponential graph, the "rate of change" increases (or decreases) across the graph.

Characteristics of Exponential Functions |
|
|
The graphs of functions of the form y = bx have certain characteristics in common.
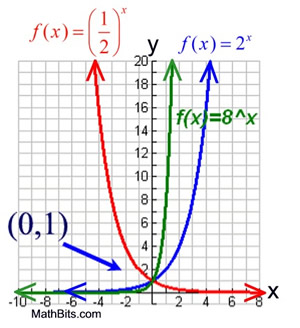 Exponential functions are one-to-one functions.
Exponential functions are one-to-one functions.
|
• graph crosses the y-axis at (0,1)
• when b > 1, the graph increases
• when 0 < b < 1, the graph decreases
• the domain is all real numbers
• the range is all positive real numbers (never zero)
• graph passes the vertical line test for functions
• graph passes the horizontal line test for functional inverse.
• graph is asymptotic to the x-axis - gets very, very close to the x-axis but, in this case, does not touch it or cross it. |

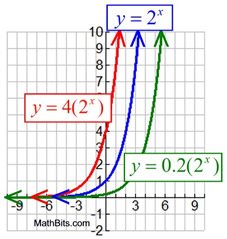
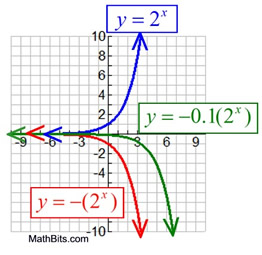
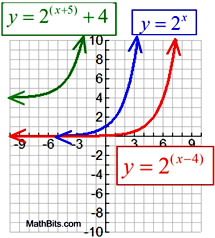
Transformations on Exponentials |
|
|
We know that transformations have the ability to move functions by sliding them, reflecting them, stretching them, and shrinking them. Let's see how these changes will affect the exponential function:
Parent function: y = bx
All 3 transformations combined: y = ab(x - h) + k

The Intercepts of Exponentials |
|
|
By examining the nature of the exponential graph, we have seen that the parent function will stay above the x-axis, unless acted upon by a transformation.
• The parent function, y = bx, will always have a y-intercept of one, occurring at the ordered pair of (0,1). Algebraically speaking, when x = 0, we have y = b0 which is always equal to 1.
There is no x-intercept with the parent function since it is asymptotic to the x-axis (approaches the x-axis but does not touch or cross it).
• The transformed parent function of the form y = abx, will always have a y-intercept of a, occurring at the ordered pair of (0, a). Again, algebraically speaking, when x = 0, we have y = ab0 which is always equal to a•1 or a. Note that the value of a may be positive or negative.
Like the parent function, this transformation will be asymptotic to the x-axis, and will have no x-intercept.
| •
If the transformed parent function includes a vertical or horizontal shift, all bets are off. The horizontal shift will affect the y-intercept and the vertical shift will affect the possibility of an x-intercept. In this situation, you will need to examine the graph carefully to determine what is happening. |
 |
The End Behavior of Exponentials |
|
|
The end behavior of an exponential graph also depends upon whether you are dealing with the parent function or with one of its transformations.
• The end behavior of the parent function is consistent.
- if b > 1 (increasing function), the left side of the graph approaches a y-value of 0, and the right side approaches positive infinity.
- if 0 < b < 1 (decreasing function), the right side of the graph approaches a y-value of 0, and the left side approaches positive infinity. |

|
• The end behavior of a transformed parent function is not always consistent, but is dependent upon the nature of the transformation. Consider this example:
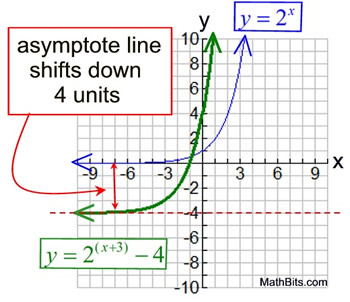 |
For the transformed equation y = 2(x+3) - 4,
the vertical shift of -4 will push the asymptote line down four units.
Thus the end behavior will be:
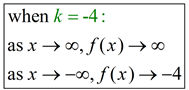
The y-intercept, where x = 0, is 4.
y = 2(0+3) - 4 = 8 - 4 = 4
The x-intercept, where y = 0, is -1.
0 = 2(x+3) - 4
4 = 2(x+3)
22 = 2(x+3)
x = -1
|

Inverse of an Exponential Function |
|
|
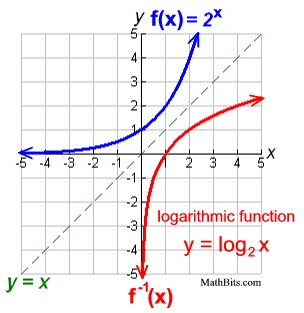
In Algebra 1, you saw that when working with the inverse of a function, the inputs (x) and outputs (y) exchange places, and that the inverse will be a reflection over the identity line y = x.
Let's take a look at the inverse of f (x) = 2x.
f (x) = 2x
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
¼ |
½ |
1 |
2 |
4 |
8 |
The inverse: f -1 (x)
x |
¼ |
½ |
1 |
2 |
4 |
8 |
f-1(x) |
-2 |
-1 |
0 |
1 |
2 |
3 |
This new inverse function is called a logarithmic function and is expressed by the equation:
y = log2 (x) |
|

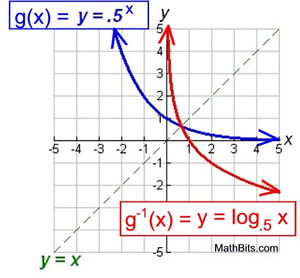
This same approach can be used to graph the inverse function when 0 < b < 1, such as y = 0.5x.
|
g(x) = 0.5x
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
g(x) |
4 |
2 |
1 |
1/2 |
1/4 |
1/8 |
The inverse: g -1(x)
x |
4 |
2 |
1 |
1/2 |
1/4 |
1/8 |
g-1(x) |
-2 |
-1 |
0 |
1 |
2 |
3 |
This new inverse function (the logarithmic function) is expressed by the equation:
y = log0.5 (x)
|
|

Solving Algebraically for the Inverses shown above:
Graph |
Inverse |
Graph |
Inverse |
|
|
|
|
y = 2x |
• set the equation equal to y |
x = 2y |
• swap the x and y |
y = log2x |
• solve for y by rewriting in log form |
|
y = 0.5x |
• set the equation equal to y |
x = 0.5y |
• swap the x and y |
y = log0.5x |
• solve for y by rewriting in log form |
|
Alternate method of finding an inverse algebraically: |
 |
|
set the equation equal to y
swap the x and y variables
take the log of both sides
apply the rule: log ar = r log a
solve for y
apply the change of base formula:
logb a = log a / log b
|

|
Interesting Application of f (x) = 2x: |
|
|
There is a well-known fable about a man from India who invented the game of chess, as a gift for his king. The king was so pleased with the game that he offered to grant the man any request within reason. The man asked for one grain of wheat to be placed on the first square of the chess board, two grains on the second square, four on the third, eight on the fourth, etc., doubling the number of grains of wheat each time, until all 64 squares on the board had been used. The king, thinking this to be a small request, agreed.
How many grains of wheat did the king have to place on the 64th square of the chess board?
Number of the doubling |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
... |
63 |
Wheat on each square |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
... |
9,223,372,036,854,775,808 |
Pattern |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
... |
263 |
In total, the king placed 18,446,744,073,709,551,615 grains of wheat on the board. This is reported to be more wheat than exists today in the entire world.
The moral of this story is, as stated by Carl Sagan, that "exponentials can't go on forever, because they will gobble up everything." One cannot treat large but finite resources as infinite.