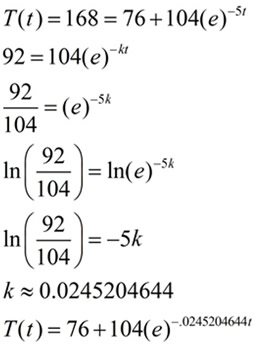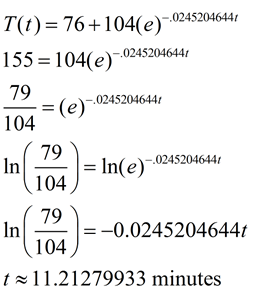In our study of Exponentials and Logarithms, we have seen various forms of exponential functions, how they behave graphically, how they are used to represent growth and decay, and how they are applied to financial situations. We are now going to take a look at how we can transform exponentials to play a role in the cooling process of liquids. Before we look at the "official formula" for Newton's Law of Cooling, let's take a look
at how we might tackle this problem with our past skills and then compare our results.
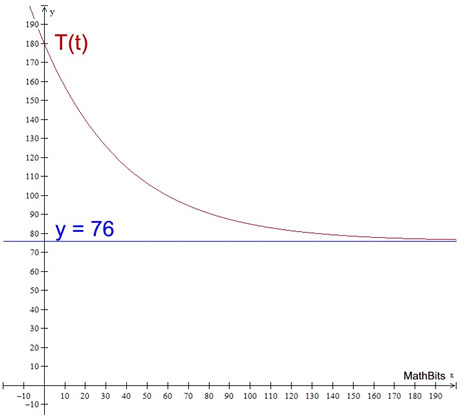
According to Newton's Law of Cooling, an object's temperature change rate is proportional to its own temperature and the temperature of the surrounding environment. The degree to which a liquid heats or cools depends largely on the ambient temperature of the environment. (Ambient means "relating to the immediate surroundings".) In a general sense, the liquid's temperature continues to change until it reaches the ambient temperature of the environment. Newton's Law of Cooling also applies to the heating of liquids in relation to the ambient temperature. One assumption about the rate of cooling or heating is that the external temperature remains constant.
If we assume that the temperature of the object is greater than the temperature of the environment, our formula will be an example of exponential decay. Let's see how using Newton's Law of Cooling works in our example. Example AGAIN: The brewing pot temperature of coffee is 180º F. and the room temperature is 76º F. After 5 minutes, the temperature of the coffee is 168º F.
If we perform a little exponent magic, we can rewrite our equation as shown below:
Comparison of the two formulas:
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||