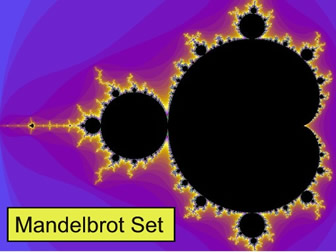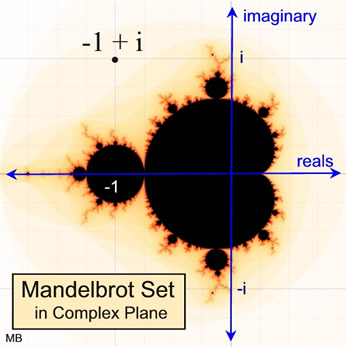
The black region is the Mandelbrot set. It is symmetric
with the x-axis and intersects the x-axis from -2 to ¼.
The Mandelbrot set consists of all of those complex c-values for which the corresponding orbit of 0 under x2 + c does not escape to infinity.
The set is named after Benoit Mandelbrot who was one of the first mathematicians to study the set in 1980. |
Infinitely Many! The decorations that adorn the main heart-shape of the set (the cardioid) are called bulbs. Each bulb in turn has infinitely many smaller decorations attached, and so on, and so on, ...
See an animated view of a Mandelbrot set. |
| An examination of the critical orbits of any complex number and the critical orbits of the complex conjugate will show a connection to the symmetric nature of the Mandelbrot set. |
|
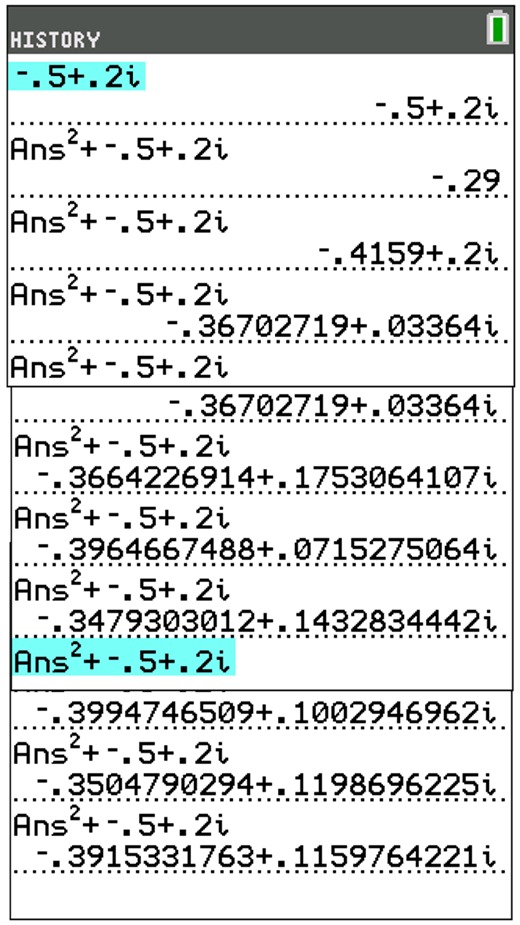
The graphing calculator can be used to help determine if the critical orbits repeat and lie in the Mandelbrot set.
Place the calculator in a + bi mode.
f (x) = x2 + (-0.5 + 0.2i )
The calculator screens below show that the iterations of this function are demonstrating a repeating nature of the orbits. This tells us that the orbits will fall in the Mandelbrot set.
If the iterations had started to grow larger and larger (escaping to infinity), the orbits would fall outside of the Mandelbrot set.
 |