|
When solving absolute value equations, think back to your first introduction to absolute value and the number line. We know that the absolute value of a number is its distance from 0 on the number line.
If | x | = 3, we know that x may be either +3 or - 3,
since both are 3 units from the origin.
Notice that the answer is "OR", since x cannot be both -3 and +3 at the same time.
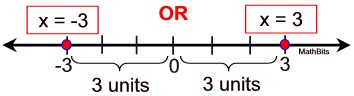
We will use this same reasoning to solve all of our absolute value equations. Notice what really happened: the absolute value expression was by itself on one side of the = sign, and we set the inside of the absolute value equal to + and to - the value on the other side of the = sign.
Let's generalize these findings:
To Solve Absolute Value Equations:
1. Isolate the absolute value expression to one side of the equal sign.
2. Set the inside of the absolute value equal to + and to - the value on the other side of the equal sign (remove the absolute value bars in this step).
3. If needed, solve for the variable in these 2 new equations.
4. Check your solutions for possible "problems" (extraneous solutions) |
|
Extraneous Solutions:
This process forms 2 new equations whose solutions may not be solutions to the original equation.
Always CHECK! |
|
Before we begin our examples, be on the lookout:
→
|
 |
Absolute value is always positive (or zero). |
An equation such as | x - 5 | = -10 is never true!
It has NO solution.
The answer is the empty set Ø. |
|
|
|
For help with solving absolute value equations
on your calculator,
click here. |
|
|
Keep in mind that your graphing calculator can be used to solve absolute value equations and/or double check your answers. |
 Solve for x: | x - 5 | = 7 [Two cases with two solutions.]
Visualize what is initially happening:
 |
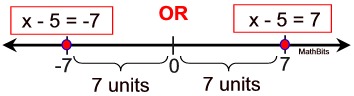Case 1:
x - 5 = 7
x = 12 |
Case 2:
x - 5 = -7
x = -2 |
Check:
| 12 - 5 | = 7
| 7 | = 7
7 = 7 |
Check:
| -2 - 5 | = 7
| -7 | = 7
7 = 7 |
The solutions are x = -2 or x = 12.
On the number line these values are each 7 units away from 5.
The distance (difference) between x and 5 is 7 units.
 |
 Solve for x: | 3x + 8 | + 5 = 2 [No solution.]
|
Look
carefully!
|
|
As soon as you isolate the absolute value expression,
you can observe that:
| 3x + 8 | = -3
There is no need to work out the two cases in this problem.
Absolute value in NEVER equal to a negative value.
This equation is never true. The answer is the empty set Ø. |
 Solve for x: | 3x + 2 | = 4x + 5 [Two cases with ONE solution.]
Case 1:
3x + 2 = 4x + 5
2 = x + 5
-3 = x
|
Case 2:
3x + 2 = -(4x + 5)
3x + 2 = -4x - 5
7x = -7
x = -1 |
The answer will be only x = -1.
The x = -3 is an extraneous solution. |
Check:
| 3(-3) + 2 | = 4(-3) + 5
| -9 + 2 | = -12 +5
| -7 | = -7
7 ≠ -7
Not a solution! |
Check:
| 3(-1) + 2 | = 4(-1) + 5
| -3 + 2 | = -4 + 5
| -1 | = 1
1 = 1
|
The check showed us that x = -3 is NOT a solution to this absolute value equation.
Always check!!! |
 In a manufacturing plant, a machine fills cereal boxes with 32 ounces of Krispy Toads cereal. After the boxes are filled, another machine weighs them. If the box's weight differs from the desired 32 ounce weight by more than 0.5 ounces, the container is rejected. Write an equation that can be used to find the heaviest and lightest acceptable weights for the Krispy Toads boxes. Solve the equation.
Solution: Let x = the weight of the cereal box.
We want to find the locations of 0.5 ounces above and below the desired 32 ounces. Common sense tells us that the answer should be 32.5 heaviest and 31.5 lightest.
Let's see if absolute value supports our answer.
| x - 32 | = 0.5
(The distance between x and 32 is 0.5 units.)
Case 1:
x - 32 = 0.5
x = 32.5
Check:
| 32.5 - 32 | = 0.5
| 0.5 | = 0.5
0.5 = 0.5 |
Case 2:
x - 32 = -0.5
x = 31.5
Check:
| 31.5 - 32 | = 0.5
| -0.5 | = 0.5
0.5 = 0.5 |
Answer: x = 31.5 ounces (lightest)
x = 32.5 ounces (heaviest) |
Remember when setting up a word problem that absolute value represents "distance" from a given point.
The difference between the answer (x) and the desired point (32) is placed inside the absolute value bars. This absolute value is then set equal to the desired "distance" (0.5).
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
