|
Rounding a measurement creates a less accurate measurement and introduces a certain amount of error in the measurement.
When dealing with measurements which have been rounded, remember what happens when rounding occurs.
|
|
|
"When rounding to a place value, look at the value immediately to the right of that position. |
If that value is 5 or bigger, round up the place value.
Otherwise, leave the place value alone."
Rounding 12.45 to nearest tenth is 12.5. Rounding 8.449 to nearest tenth is 8.4. |
If a rounded measurement is given, to the nearest tenth, to be 9.5 inches, then the acutal measurement could be 9.48 inches, or 9.535 inches, or 9.5488 inches, or 9.51 inches, and so on. The actual measurement could be anywhere in a range of values which all round to 9.5. The actual measurement can be no smaller than 9.45 (or it won't round to 9.5). On the larger end, the actual measurement can be any value up to, but not including 9.55. The 9.55 would round to 9.6. Remember, also, that values such as 9.5499999 round to 9.5.
 Don't round too soon!!
NOTE: When a problem calls for a rounded answer, be sure to perform all of your calculations first and round ONLY the final answer.
If you continually "round" separate calculations within A problem, larger and larger accuracy errors will be produced. |
 The exact dimensions of a rectangular bulletin board are 3.5 meters by 1.8 meters. The fabric needed to cover the board costs $12.35 per square meter. To the nearest dollar, find the cost of covering the board with the fabric.
|
ACTUAL ANSWER: 3.5 x 1.8 x 12.35 = 77.805 when rounded becomes $78.
ANSWER with COST ROUNDED: 3.5 x 1.8 x 12 = 75.6 when rounded becomes $76.
ANSWER with ALL VALUES ROUNDED: 4 x 2 x 12 = $96.
The more rounding that was done before the computations, the less accurate the answer became.
Be careful when working with rounding and area!!
The dimensions of the floor of a garage measure 22 feet by 24 feet, rounded to the nearest foot.
What is the range of values that could represent the actual area of the garage floor?
ANSWER:
The actual measurements of the lenth and width fall into the ranges:
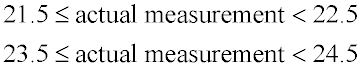
The smallest possible area = (21.5)(23.5) = 505.25 square feet.
The largest possible area < (22.5)(24.5) < 551.25 square feet.
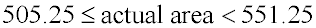
 and
the calculator |
When working with formulas that
involve
such as:
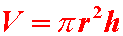
remember that using the
key on the calculator will give a different answer than using the
approximation of 3.14.
Using the
key will give a more accurate answer. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
