Linear Programming (also called "linear optimization") is an application of mathematics used in real-life areas such as engineering, economics, business, industry, and social science.
Graphs of inequalities (the "constraints") are used to create a "feasibility region" (a polygon-shaped area on the graph). Feasibility regions are all locations that represent "feasible" (possible, correct, viable) solutions to the system of inequalities. Maximum and minimum values for an "objective" function can then be established based upon the values obtained at the "corners" (intersection points, vertices) of the feasibility region.
 To establish the feasibility region: To establish the feasibility region: |
1. Graph the given system of inequalities to form the "feasibility region" (a walled-off area, a polygon-shaped area) on the coordinate axes. The feasible region may have three, or more, sides.
2. Determine the coordinates of each of the vertices of the polygon-shaped area on the graph (the feasible region).

Once the feasibility region has been established, linear programming then examines a function which is to be maximized or minimized withing this feasible region. The coordinates of each vertex of the feasible region is substituted into the function. The largest result is the maximum value, and the smallest result is the minimum value of the function based upon this region.

a.) Find the feasibility region for the system of inequalities at the right.
b.) State the coordinates of the "corners" of the region.
|
|
1. Graph the three inequalities, shading appropriately. Locate the area where the three shadings overlap. In this example, the overlapping feasibility region (the polygon) is a triangle.
2. Find the corner points (the points of intersection) of the polygon-region (the feasibility region).
The corner points for this example are:
(-2,2), (8,7), and (8,2).
|
|
Let's assume that the function f (x,y) = z = x - 4y is to be maximized or minimized within the feasible region from Example 1.
Each vertex of the feasible polygon is tested into function, z.
Test (-2,2): (-2) - 4(2) = -2 - 8 = -10
Test (8,2): (8) - 4(2) = 8 - 8 = 0
Test (8,7): (8) - 4(7) = 8 - 28 = -20 |
Under the constraints of this system of inequalities:
the function is maximized at (8,2) with a value of 0; and
the function is minimized at (8,7) with a value of -20.

Jason custom paints snowboards and snowmobiles. It takes 5 hours to paint a snowmobile and 2 hours to paint a snowboard. The profit on a snowmobile is $35 and on a snowboard is $10. Jason can only spend 19 hours a week on this custom painting, and must paint at least 1 snowmobile and 2 snowboards each week. How many snowmobiles and snowboards should Jason paint each week to maximize his profit? What is his maximized profit? |
1. Identify the variables in the problem.
|
Let x = number of snowmobiles
y = number of snowboards
p = profit
|
2. Determine the inequality constraints.
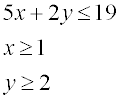
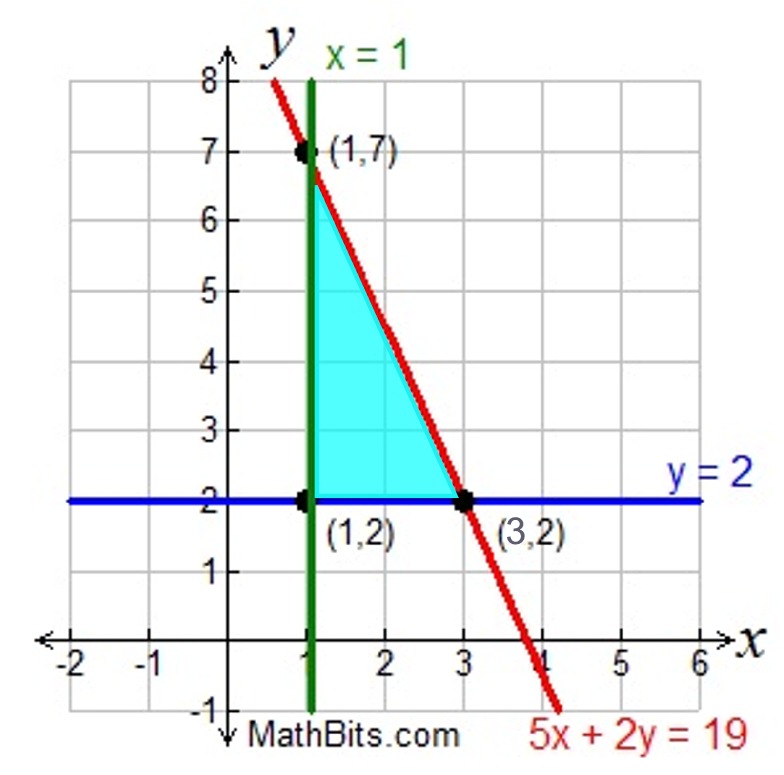
Graph the inequalities to find the feasibility region. Find where the shading overlaps.
Find the corner points (the points of intersection) of the polygon-region (the feasibility region).
The corner points for this example are:
(1,2), (1,7), and (3,2).
|
 |
3. Determine the objective function.
p = 35x + 10y
Test the corner points to determine the maximum value for the function under the constraints of these inequalities. |
Test (1,2): 35(1) + 10(2) = 55
Test (1,7): 35(1) + 10(7) = 105
Test (3,2): 35(3) + 10(2) = 125 MAX.
He should paint 3 snowmobile and 2 snowboards per week to maximize his profits (which will be $125). |
|