Practice Page
Directions: Read carefully and choose the best answers.
1. The two-way frequency table, shown below, displays the data collected from a random group of high school students regarding whether they "liked" skateboards and/or "liked" snowmobiles. Answer the questions below, regarding this table.
2wayprac1
a.  How many students participated in the survey?
Choose:
55
105
125
160

b. How many students said they "like" snowmobiles?
Choose:
25
80
105
125

c. Which of the following values is referred to as a "marginal frequency"?
Choose:
10
25
35
45

d. How many of the students "like" snowmobiles, but "do not like" skateboards?
Choose:
10
25
35
45

e. How many students said they "do not like" skateboards?
Choose:
10
25
35
55

divider

 

2. Freshman girls and boys were surveyed to choose their favorite subject from the list of Math, English or Science. The results are shown in the two-way relative frequency table below (rounding to nearest hundredth). Answer the questions below, regarding this table.
2wayprac2
a.  How many girls participated in the survey?
Choose:
50
60
150
315

b. What percentage of the boys chose "Science"?
Choose:
41%
42%
4.1%
4.2%

c. This table shows relative frequencies based upon ______.
Choose:
the whole table
the rows
the columns

d. What percentage of the girls chose "Math"?
Choose:
27%
33%
39%
40%

e. What percentage of the students chose "English"?
Choose:
27%
18%
22%
41%

divider

 

3. You are testing a theory that says that students who speak a foreign language are also strong mathematics students. You survey the freshman class and the results are shown below, in an incomplete two-way frequency table. Answer the questions below, regarding this table. Percentage answers rounded to nearest percent.
2way3prac
a.  How many students were surveyed?
Choose:
65
85
145
80

b. What percentage of the students speak a foreign language and have a math average greater than or equal to 90?
Choose:
41%
48%
82%
88%

c. What percentage of the students with a math average greater than or equal to 90 do not speak a foreign language?
Choose:
10%
18%
23%
25%

d. How many of the students do not speak a foreign language?
Choose:
15
50
60
65

e. Does the table appear to support the theory that students who speak a foreign language are also strong mathematics students? Explain.
Choose:
Yes
No

divider

 

4. Allison collected data to see if there was a relationship between students having blue eyes and the students wearing yellow on the day of the survey. She randomly surveyed the freshman class and the results are shown below. Answer the questions below, regarding this table. Percentage answers rounded to nearest percent.
2wayprac4
You will need to prepare row conditional relative frequencies for this table.
a.  What are the row conditional relative (joint) frequencies, from left to right, for the category "Blue Eyes"?
Choose:
16%; 3%
83%; 17%
20%; 4%
75%; 25%

b. What percentage of "Not Blue Eyes" students were "Not Wearing Yellow"?
Choose:
20%
30%
40%
45%

c. Is there a sufficient difference in the row conditional relative frequencies to statistically imply an "association" between Blue Eyes and Wearing Yellow? Explain.
Choose:
Yes
No

divider

 

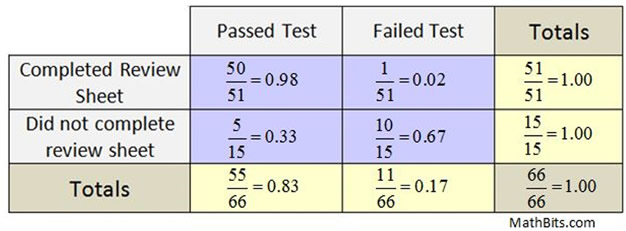
5. The test results of 66 students were compared with whether the students completed a review sheet provided by their teacher prior to taking the test. A row conditional relative frequency table was prepared. (rounded to nearest hundredth)
chartt5
a.  Explain whether the table indicates a statistical association between completing the review sheet and passing the test.


b. If an association between completing the review sheet and passing the test exists, would it imply that completing a review sheet will improve test scores for ALL students everywhere? Explain.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".