|
Directions: Solve the following problems dealing with statistical graphs.
|
1. Questions pertain to the histogram shown below. |
|
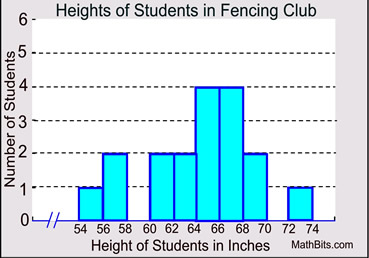 |
(c) What percentage of the students have a height greater than or equal to 60 inches but less than 66 inches, to the nearest tenth of a percent?
|
(d) In which interval, will you find the median student height, h?
Choose:
|
|
|
2. The box and whisker plots below represent the number of points scored in each game for the fall football season for two area high school teams. |
(b)Which team's data shows more variability in the points scored?
(c) What is the difference between the median points scored by these two teams?
|
|
|
3. In the same morning, fifteen people spend money on $5 lottery tickets at a local gas station. The dot plot shows the amount spent by each customer on the tickets.
|
|
|
|
|
(b) What is the mean (average) of the dollars spent?
(c) What monetary value represents the first quartile of this data?
|
(d) What is the interquartile range?
|
(e) What is the sample standard deviation for this data (to the nearest hundredth)?
|
|
4. The box and whisker plots shown below represent monthly temperatures (º F) for three cities. |
|
|
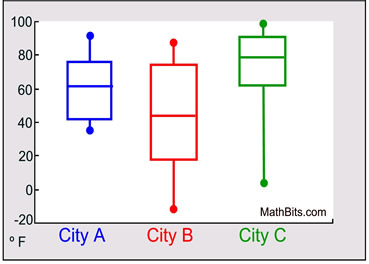 |
|
|
5. Examine the histograms shown below. Complete the chart below by choosing the graph that best shows the stated result. |
|
| |
Graph A |
Graph B |
Both Graphs |
Larger Median |
|
Symmetric Graph |
|
Smaller Range |
|
Larger Data Count |
|
Interval Scale of 2 |
|
|
|
6. Two game players have been recording their best scores each day during a one week video tournament. Based on the box plots shown below, determine if the following statements are true or false. |
(a) The median score of Player A is greater than the median score of Player B.
(b) The highest score was obtained by Player B.
|
|
(c) The interquartile range of the scores of Player B is less than the interquartile range of the scores of Player A.
|
|
7. Examine the dot plots shown below. Complete the chart below by comparing the two plots. |
|
| |
Larger in
Data X |
Same in
both
data sets |
Larger in
Data Y |
Median |
|
Range |
|
Mean |
|
Standard Deviation |
|
Mode |
|
Maximum |
|
Show how to verify that 10 is an outlier Data X.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|