|
 |
A measure of central tendency (measure of center) is a value that attempts to describe a set of data by identifying the central position of the data set (as representative of a "typical" value in the set). |
We are familiar with measures of central tendency called the mean, and median.
Let's examine the mean as a "balance point" in the ordered data set.
Consider:
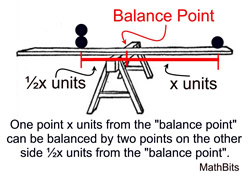
The mean of a distribution can also be thought of as a "balance point" for the distribution. The sum of the distances to the right of the mean equals the sum of the distances to the left of the mean.
Think of the mean as the fulcrum for a seesaw. The balancing of the seesaw depends upon the number of items and their distances from the fulcrum.
|
|
Example: Given the data set: {1, 4, 5, 5, 7, 8, 11, 11, 11}
(In this data set the mean = 7 and the median = 7.) |
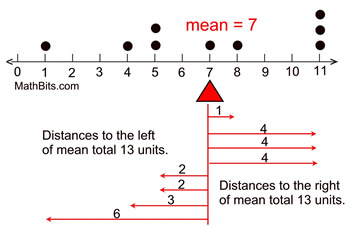
It is always true that the total distance below the mean
is equal to the total distance above the mean. |
|
|
|
Graphically speaking, the "center" of a distribution is located at the median of the distribution.
The median is the point where half of the data points are found on its left side and half on its right side. While the median indicates the "center", it may not always represent the most "typical value" in the data set. Let's see which measures of center represent the most typical values of the data given various situations.
Which measures of center are representative of the most typical values in the data set?
|
Distribution |
Central Tendency |
Typical Graph |
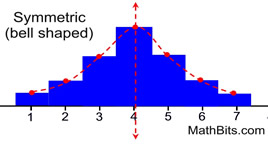
Bell-shaped
Symmetric Distribution
|
The mean, mode and median will be the same value.
• Best measure of center:
mean
|
 |
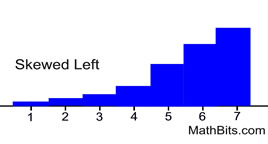
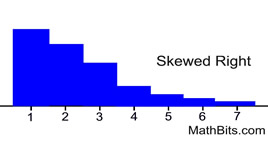
Distribution Skewed Right
|
Typically has
mean > median
There may be exceptions to this statement.
• Best measure of center: median
|
 |
|
|
Typically has mean < median
There may be exceptions to this statement.
• Best measure of center: median |
|
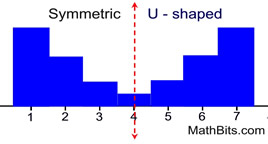
U-shaped Symmetric Distribution
|
Neither the mean nor the median is a good indicator of typical values in the set.
• Best measure of center:
midrange*
- but the mean as a "balance point" is also a "descriptor" of the center of the distribution
|
|
*FYI: There is another less popular measure of center called the midrange.
The midrange is the average of the maximum and minimum values of the data set,
which is actually the midpoint of the range.
The midrange is not widely used since it is dependent upon only two values in the set.
Unfortunately, measures of central tendency alone may be insufficient to truly describe the typical data in a set.
It is possible that two data sets can have the same mean, but be very different kinds of sets. It is best to use measures of central tendency, along with other observations of the data set, to best describe the data set.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|