The properties of the Real Number System are useful when working
with equations, functions and formulas in Algebra.

These properties allow for the creation of equivalent expressions.

Name a property of real numbers which justifies: -5 + (4 + a) = (-5 + 4) + a

This example deals with addition between all of the terms and with "grouping" ("association") of terms using parentheses. Notice that the terms remain in the same order. Only the positioning of the parentheses has changed. This is the Associative Property of Addition.

Explain why these expressions are equivalent. m + (n + x) = m + (x + n)

This example also deals with addition between all of the terms. Unlike the first example, however, these terms do not remain in the same order. The terms within the parentheses have switched places ("commuted"). This is the Commutative Property of Addition.

Using the Distributive Property, rewrite: 8(x - 6)

The Distributive Property multiplies (distributes) a term across the added terms within a set of parentheses. While this example looks like "subtraction" within the parentheses, it can also be re-written as "addition" of a negative value, 8(x + (-6)). Always multiply ALL of the terms within the parentheses and be careful of the signs. This solution will be 8•x + 8•(-6) = 8x - 48.

Rewrite using the Distributive Property. -7p - 49

Since there are no parentheses in this problem, it must be the result of the Distributive Property having already been "distributed" across a set of parentheses. We need to work backward!
This is the Distributive Property in reverse. Look for a common factor between the terms.
In this case, -7 will do nicely.
This solution will be (-7)(p) + (-7)(7) = -7(p + 7).
Always check your final answer on these problems by multiplying through.

The area of rectangle ABCD can be expressed using its full exterior measurements or as the sum of the areas of the two smaller rectangles. Write an equation showing these two equivalent expressions, and state which property is being illustrated.

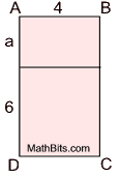The area of rectangle ABCD can be expressed as 4(a + 6).
The sum of the areas of the two smaller rectangles can be expressed as 4a + 4•6.
Equation:    4(a + 6) = 4a + 4•6       The Distributive Property.

The properties of the Real Number System are also used to help explain or justify solutions.

Justify the steps in the simplification of this expression. 8 + 5(x - 2) - 3x + 9

A property of the Real Numbers is used to progress from one step to the next.

8 + 5(x - 2) - 3x + 9	Given
8 + 5x - 10 - 3x + 9	Distributive Property
8 + 5x - 3x - 10 + 9	Commutative Property of Addition
8 + x(5 - 3) - 10 + 9	Distributive Property in reverse
8 + x(2) -1	Numerical simplification
8 + 2x - 1	Commutative Property of Multiplication
8 - 1 + 2x	Commutative Property of Addition
7 + 2x	Numerical subtraction

And sometimes these properties just make computations easier.

Evaluate: 76 x 8 - 73 x 8 without a calculator.

Using the Distributive Property in reverse, this expression can be written as (76 - 73) x 8 which is 3 x 8 = 24. EASY!!!