We have seen how the process of simplifying radicals works with numerical values. Now, let's see what happens when algebraic variables are involved.
[On this page, the radicand will be non-negative. No negatives under the radical. Also, all variables will be positive.]

Simplifying Algebraic Square Roots: |
|
A square root is in simplest form when
1.
the radicand contains no perfect square factors
2. the radicand is not a fraction
3. there are no radicals in the denominator of a fraction. |
Before we begin, take a minute to look at the first table at the right called "Perfect Squares". Notice how variables are perfect squares when their exponents are even numbers. Also, remember the exponent rule, xa • xb= xa + b.

 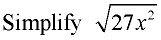
1. First, we will separate the number value from the algebraic variable. This will give us a chance to examine each for perfect square factors.
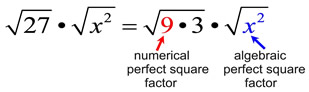
2. Give each factor its own radical symbol. 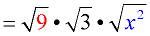
3. Reduce the "perfect square" radicals. 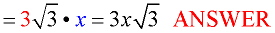

 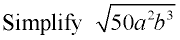
Separate and find the largest perfect square factors.
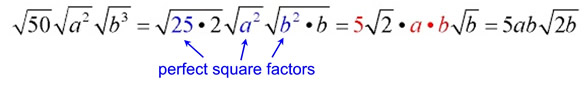
 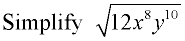
Separate and find the largest perfect square factors. Remember that even numbered exponents are perfect squares.

 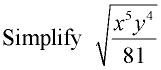

The quotient rule was applied and the perfect square factors found.
 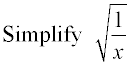
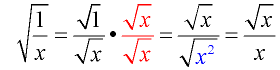
The denominator is being rationalized by multiplying by the denominator radical value.
Simplifying Algebraic Cube Roots: |
Before we begin, take a minute to look at the third table up from the bottom at the right showing algebraic "Perfect Cubes". Notice how variables are perfect cubes when their exponents are multiples of three.
Again, remember the exponent rule, xa • xb= xa + b.
 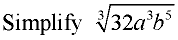
Remember you are dealing with perfect cubes (not perfect squares). Separate and find the perfect cube factors.


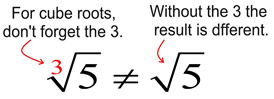
When working with cube roots, it is easy to forget to write the index value of 3 on the symbol. Be careful! Without the 3 written in the cube root symbol, your answer will be incorrect, as it represents a different value.
|