In this lesson, the term "radical" will refer to "square root".
Adding or subtracting radicals is the same concept as that of adding or subtracting similar, or "like", terms. The index and the values under the radical (the radicands) must be the SAME (creating "like radicals") before you can add or subtract the radical expressions.
|
Adding and subtracting radicals: For radicals having the same index (root) and the same values under the radical (the radicands), add (or subtract) the values in front of the radicals and keep the radical. |
|
 |
When the radicals in an addition or subtraction problem are different, check to see if the radicals can be simplified.
It may be the case that when the radicals are simplified, they will become "like" radicals which can be added or subtracted.
|
 REMEMBER: Always simplify first, if possible! |
Simplify the radicals - then combine like terms!
|
|
|
ANSWER:  |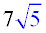
| |
Since the radicals are the same, add the values in front of the radical symbols, and keep the radical. Do NOT add the values under the radicals. Think of having three of the radical 5s, adding 4 more of the radical 5s, and getting a total of 7 radical 5s.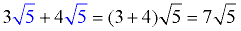 
|
|
|
ANSWER:  |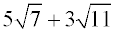
| |
The radicals are different and each is already in simplest form. There is simply no way to combine these values. The answer is the same as the original problem.
|
|
|
ANSWER:  |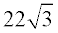
| |
At first glance, it appears that combining these terms under addition is not possible since the radicands are not the same. But if we look further, we can simplify the second term so it will be a "like" radical:
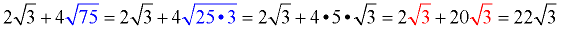
We simplified the second radical to 20 radical 3, making it a "like" radical. We were then able to add the terms.
|
|
|
ANSWER:  |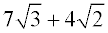
| |
There is an implied "1" in front of 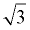 . All radicals are already in simplest form. Combine the "like" radicals.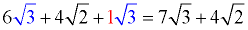 
Don't be afraid to list an answer with more than one "different" radicals.
|
|
|
ANSWER:  |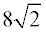
| |
Simplify the radicals first, and then subtract and add.
|
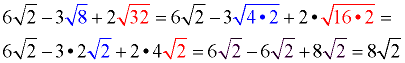
Extra
|
|
ANSWER:  |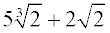
| |
FYI. What happens if you try to add radicals with different indexes?
Notice that this problem mixes cube roots with a square root. The same type of approach is used to add cube roots as is used to add square roots, however the cube roots and square roots cannot be combined with one another through addition.
Notice that the answer keeps the cube root and square root separate.
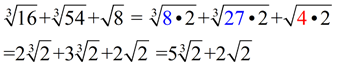
You cannot combine cube roots and square roots through addition or subtraction, even after being simplified.
They are not "like radicals" since their roots are different.
|
|
|
