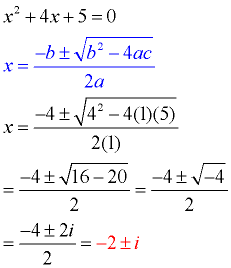|
We started a brief investigation of imaginary numbers and complex numbers back in the Radical section. Let's now take a quick look at how these numbers relate to quadratics and graphing.
Imaginary numbers and complex numbers will be studied in Algebra 2.
|
The imaginary unit (number) is i. |
|
| |
An imaginary number is a number whose square is negative. |
|
 Clarification on vocabulary:
pure imaginary number
"bi "
A pure imaginary number can be written in bi form where b is a non-zero real number and i is the imaginary i.
Examples:
3i, -6i,  ,  |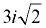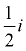
complex number
"a + bi "
A complex number may appear as any real number a, a pure imaginary number bi, or the sum of both.
Examples: 8 (which is 8 + 0i), 6i (which is
0 + 6i), 3 + 9i, -2 - 5i,
|
The set of real numbers and the set of imaginary numbers are subsets of the the set of complex numbers. |
Quadratic Equations and Roots Containing "i ":
In relation to quadratic equations, imaginary numbers (and complex numbers) occur when the value under the radical portion of the quadratic formula is negative. When this occurs, the equation has no roots (zeros) in the set of real numbers. The roots belong to the set of complex numbers, and will be called "complex roots" (or "imaginary roots"). These complex roots will be expressed in the form a + bi.
Consider this example:
Find the roots: x2 + 4x + 5 = 0
This quadratic equation is not factorable, so we apply the quadratic formula. Notice that after combining the values, we are left with a negative value under the square root radical. This negative square root creates an imaginary number.
|
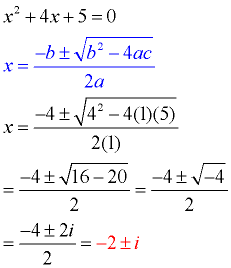
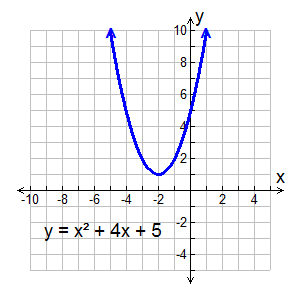The graph of this quadratic function shows that there are no real roots (zeros) because the graph does not cross the x-axis. Such a graph tells us that the roots of the equation are complex numbers, and will appear in the form a + bi. |
Did you notice ...
The complex roots in this example are x = -2 + i and x = -2 - i. These roots are identical except for the "sign" separating the two terms. One root is -2 PLUS i and the other root is -2 MINUS i. This pattern will occur in every set of complex roots that you will encounter when solving a quadratic equation. Roots that possess this pattern are called complex conjugates (or conjugate pairs).
|
When graphing, if the vertex of the quadratic function lies above the x-axis, and the parabola opens upward, there will be NO x-intercepts.
This graph will have complex roots (a + bi form).
Also applies if the vertex lies below the x-axis, and opens down. |
|
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
