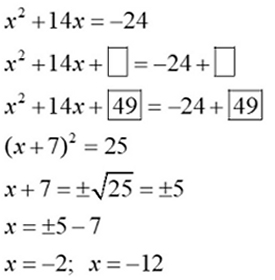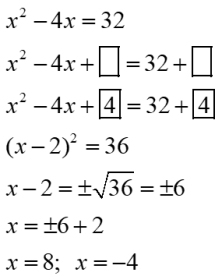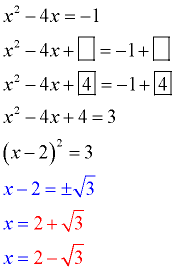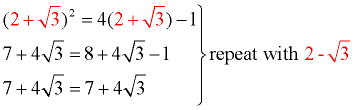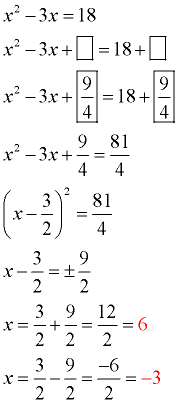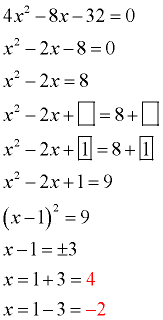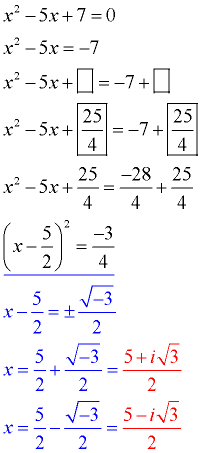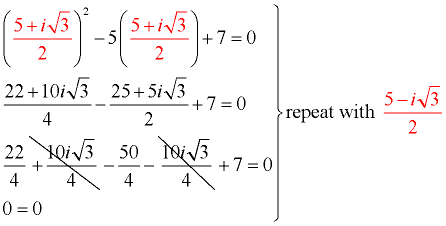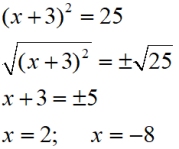The leading coefficient is NOT 1, but it can be 1 by dividing each term in the equation by that leading coefficient (in this case, divide through by 4).
Divide all terms by 4 (the leading coefficient). In this example, 4 is the GCF of all of the terms, so "nice" integers will emerge.
[ Note: In some problems, this division process may create fractions, which is OK. Just be careful when working with the fractions.]
Move the constant to the right hand side.
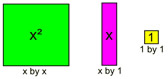
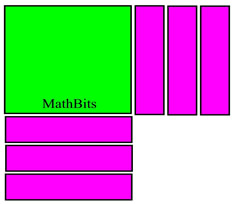
Prepare the equation to receive the added value (boxes).
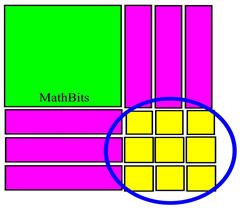
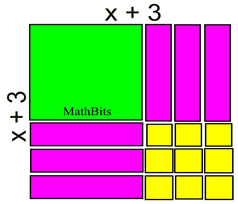
Take half of the x-term's coefficient and square it. Add this value to both sides (fill the boxes). Combine like terms.
Factor the perfect square trinomial on the left side.
Take the square root of both sides. Be sure to consider "plus and minus".
Solve for x. Clearly indicate your answers.
Prepare a check of the answers.
4(4)2 - 8(4) - 32 = 0 check
4(-2)2 - 8(-2) - 32 = 0 check |