|
 Can you determine the equation of a quadratic given its solutions? If you are given the solutions of an equation, you can find an equation by working backward.
1. a. Determine an equation that has the solutions x = -4 and x = 3.
Work backward to find the equation: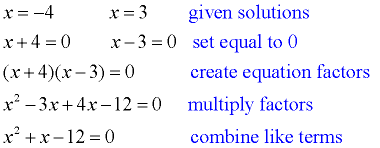
We now have an equation answer:
x2 + x - 12 = 0 |
1. b. Find the solutions for the equation 3x2 + 3x - 36 = 0.
This equation can be solved by factoring.
|
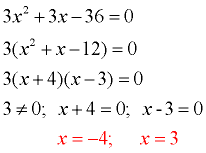
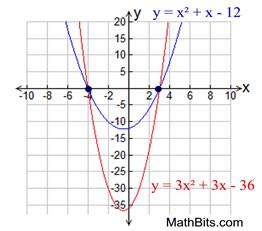
Conclusion:
Working backward will create an equation, but remember that there are other equations that will also have that same set of solutions.
(Compare the solutions in 1a with 1b, and take a look at the graph at the right.)
Any equation of the form k(x2 + x - 12) = 0, where k is a constant, has the same solutions as
x2 + x - 12 = 0.
|
 |
|
If you have the graph of a parabola, can you determine the equation
of the function that created the graph?
Let's see what's possible.
1. Given the naked parabolic graph at the right, you are told that the x-intercepts and y-intercept are integer values.
Thankfully, the graph shows a scale where each displayed unit on the x and y axes represents one unit.
Since we know that the x-intercepts are integer values, we can read them off the graph to be (-3,0) and (4,0).
|
|
If the x-intercepts are (-3,0) and (4,0), we know that the roots (zeros) of the equation will be x = -3 and x = 4. Working backward, we can create the factors (x + 3) and
(x - 4) and get the equation y = (x + 3)(x - 4).
BUT... do we know for sure that there is no numeric factor in this equation? Could it be, for example, y = 2(x + 3)(x - 4), since this equation also has zeros of x = -3 and x = 4 ?
We need to check another point. The only observable point is the y-intercept (0,-12).
Since (0,-12) is on this graph, it will satisfy the equation of the graph.
Our First Equation:
y = (x + 3)(x - 4).
-12 = (0+ 3)(0 - 4).
-12 = -12 TRUE |
Possible Other Equation:
y = 2(x + 3)(x - 4)
-12 = 2(0 + 3)(0 - 4)
-12 ≠-24 FALSE |
Our first equation is
the answer:
y = (x + 3)(x - 4) or
y = x2 - x - 12 .
|
|
|
The zeros obtained from the x-intercepts of a graph can determine the equation of a "family" of graphs. But, ONE MORE POINT is needed to guarantee a specific, individual function's equation. |
2. Given the parabolic graph at the right, where it is known that the turning point is (2,-3) and another random point on the graph is (5,6). Write the equation of the function which created the graph.
It does not appear that the roots (zeros) of this parabola cross the x-axis at integer values, so the approach we used in the first example will not work here. |
|
We will use the vertex form: y = a(x - h)2 + k. We know the vertex is (2,-3) = (h,k), so h = 2 and k = -3. If we substitute, we get y = a(x - 2)2 + (-3).
Now, what about "a" ? We know that the point (5,6) is on the graph, which means that if we substitute x = 5 into the graph's equation, we will get a y-value of 6.
y = a(x - 2)2 + (-3)
6 = a(5 - 2)2 + (-3)
6 = 9a - 3
9 = 9a
1 = a |
The value for a in this problem is "1".
The equation is: y = (x - 2)2 + (-3).
You cannot assume that the a-value will always be 1.
|
|
There are additional methods for creating equations from graphs
that will be discussed in Algebra 2.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
