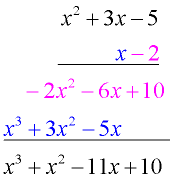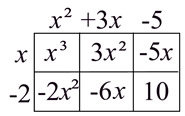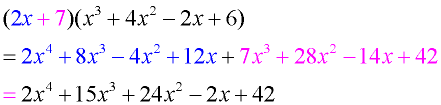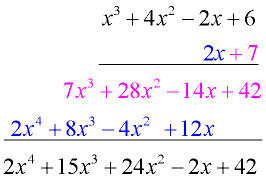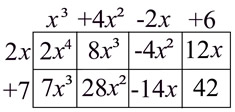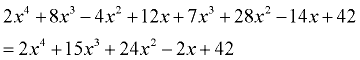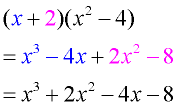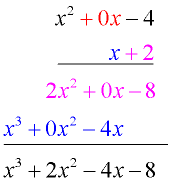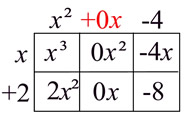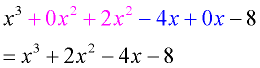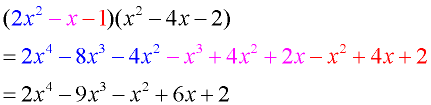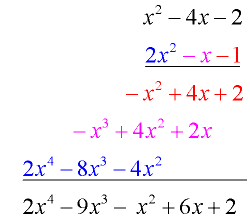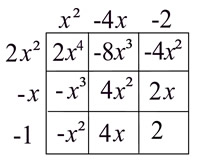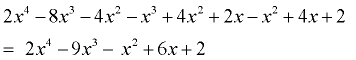|
|
A "polynomial" may contain one term (monomial), two terms (binomial), three terms (trinomial), or more terms. |
We have seen monomials multiplied by other polynomials, and binomials multiplied by binomials.
Now, let's see what happens when other combinations of polynomials are multiplied.
|
There are various set-up methods possible when multiplying polynomials. As the number of terms in the polynomials increases, the vertical multiplication set-up is much more likely to yield a correct result. It neatly organizes your work which helps eliminate careless errors. |
The following examples will show various set-up methods for the multiplications.
 Notice that "FOIL" will not work to solve any of these problems.
Multiply: (x - 2)(x² + 3x - 5) (binomial x trinomial) |
Vertical Set-Up: Line up the polynomials as you would for numerical multiplication. Be careful of your signs.
|
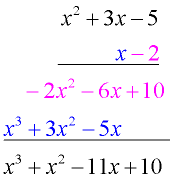
Horizontal Set-Up: Multiply each term of the binomial times each term of the trinomial. There will be 6 multiplications. Combine the like terms.
|
Grid Set-Up:
•
Place one of the polynomials along the top and the other down the left side.
•
Position the terms so that each term (and its sign) lines up with a row or column of the grid.
•
Multiply each intersecting row and column to fill the interior of the grid.
• Copy and add all of the terms in the interior of the grid.
•
Combine like terms. |
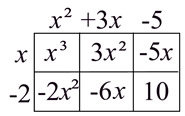
x³ + 3x² - 5x - 2x² - 6x + 10
= x³ + x² - 11x + 10
|
|
Multiply: (2x + 7)(x³ + 4x² - 2x + 6) (binomial x 4-term polynomial) |
Horizontal Set-Up: Multiply each term of the binomial times each term of the cubic polynomial. There will be 8 multiplications. Combine the like terms.
|
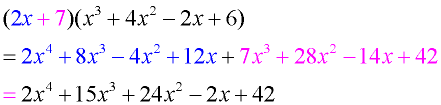
Vertical Set-Up: Line up the polynomials as you would for numerical multiplication. Be careful of your signs.
|
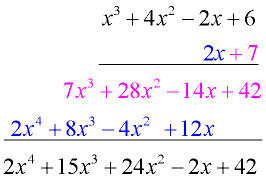
Grid Set-Up: Set up the grid and multiply.
|
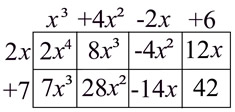
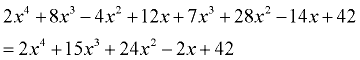
Multiply: (x + 2)(x² - 4) (missing term in second factor) |
Horizontal Set-Up: Multiply each term of the binomial times each term of the cubic polynomial. There will be 8 multiplications. Combine the like terms.
|
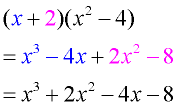
Vertical Set-Up: Line up the polynomials as you would for numerical multiplication. Be careful of your signs. If a term is missing, replacing it with 0 (such as 0x in this example) may help you to line up the terms correctly.
|
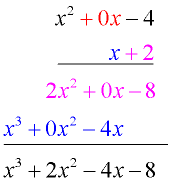
Grid Set-Up: Set up the grid and multiply.
Including the missing term will keep the diagonals working properly in the grid for adding purposes.
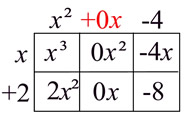
Combining the terms by adding along the diagonals: |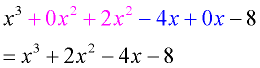
Multiply: (2x² - x - 1)(x² - 4x - 2) (trinomial x trinomial) |
Horizontal Set-Up: Multiply each term of the first trinomial times each term of the second trinomial. There will be 9 multiplications. Combine the like terms.
|
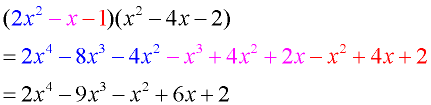
Vertical Set-Up: Line up the polynomials as you would for numerical multiplication. Be careful of your signs.
|
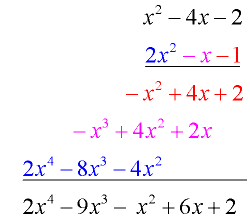
Grid Set-Up: Set up the grid and multiply.
|
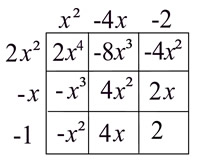
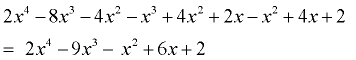
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
