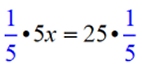Justify Solutions to Linear Equations MathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

When you solve an equation, you use a process called deductive reasoning where you apply ideas that you know to be true. For example, you know that if you add the same number to both sides of an equation, the equation will not be changed. Many of the "ideas" that you use when solving are, in actuality, the mathematical properties (rules) that we saw in Real Numbers and Properties.   Using real number properties (such as the commutative, associative, and distributive properties) and the properties of equality (such as adding, subtracting, multiplying and dividing by a non-zero) justify why each step in the process of solving a linear equation is legal!

Let' start with an easy example, so we can see what needs to be done.

Steps:	Justification (Reasons):
5x + 4 = 29	given equation
5x + 4 - 4 = 29 - 4	Subtraction Property of Equality subtract the same value from both sides of = sign
5x = 25	Additive Inverse Property (left) + 4 - 4 = 0 Numerical Subtraction (right) 29 - 4 = 25
	Multiplication Property of Equality multiply both sides of = sign by the same value
x = 5	Multiplicative Inverse Property (left) 5 • 1/5 = 1 Numerical Division (right) 25 ÷ 5 = 5

Yes, in the fourth step, you could have divided both sides by 5 and used "Division Property of Equality". The only drawback is that the needed "multiplicative inverse" reasoning in the fifth step would not be as "obvious" to someone reading your justification.
Some people may say that you would need to add a statement such as
"division by 5 is equivalent to multiplication by 1/5".
I know, picky, picky, picky. When in doublt, ask your teacher what is expected.

Let's now try something a little more challenging.

The justification method shown above is an example of one method.
In this method, the expression "Combine Like Terms" was used.
"Combine Like Terms" can actually be broken down further using other
Real Number properties which will be shown in the next example.

Let's see how we can analyze "combine like terms".
This is a more intense breakdown of the properties involved.

"Combining Like Terms" is broken down using reverse Distribuive Property, Addition, and Commutative Property.

Solve for x and justify each step with a reason: 4x - 1 + 5x = 12x - 22

Steps:	Justification (Reasons):
4x - 1 + 5x = 12x - 22	Given statement
4x + 5x - 1 = 12x - 22	Commutative Property of Addition
x(4 + 5) - 1 = 12x - 22	Distributive Property in reverse
x(9) - 1 = 12x - 22	Numerical Addition
9x - 1 = 12x - 22	Commutative Property of Addition
9x - 9x - 1 = 12x - 9x - 22	Subtraction Property of Equality
x(9 - 9) - 1 = x(12 - 9) - 22	Distributive Property in reverse
x(0) - 1 = x(3) - 22	Additive Inverse Property (left side) 9 - 9 = 0 Subtraction (right side) 12 - 9 = 3
0 - 1 = 3x - 22	Zero Property of Multiplication (left side) x(0) = 0 Commutative Property of Multiplication (right) x(3) =3x
- 1 = 3x - 22	Additive Identity Property
-1 + 22 = 3x - 24 + 22	Addition Property of Equality
21 = 3x + 0	Numerical Addition (left side) Additive Inverse Property (right side)
21 = 3x	Additive Identity Property
(1/3) • 21 = 3x • (1/3)	Multiplicative Property of Equality
7 = x	Numerical Multiplication (left) Multiplicative Inverse Property (right)