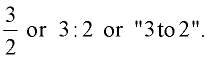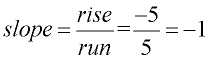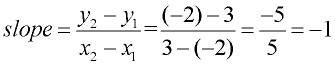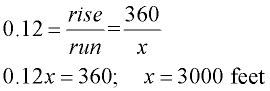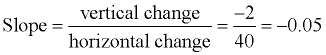|
Slope is used to describe the measurement of steepness of a straight line.
In different situations, slope may be referredt to as incline, pitch, or grade (gradient).
Slope is also described as a rate of change.
Slope can be expressed in various ratio forms: 
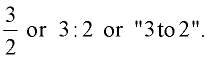Slope is traditionally designate by the letter "m".
 Let's see what slope looks like graphically:
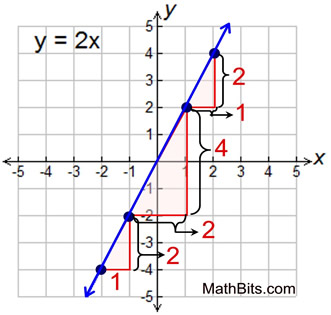
Consider the line y = 2x.
Notice the desginated points on the line. The ratio of your vertical movement (rise) to get from one point to another, over the horizontal movement (run), will always be the same.
The "rise" over "run" for this graph is 2 over 1. For every one unit moved on the x-axis, two units are moved on the y-axis.
From any point, movements to the right and up are positive, while left and down are negative.
For any two-points chosen, the vertical change over the horizontal change is in the ratio of 2:1.
(Remember that 4/2 = 2/1.) |
The rate of change on a straight line is constant
(always the same). |
Example:
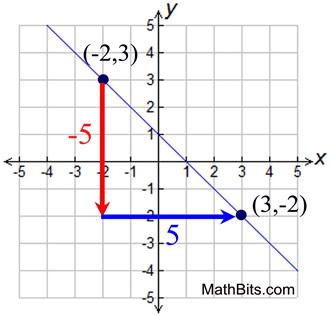
Find the slope of a line passing through the points (-2,3) and (3,-2).
• If you graph the points, you can "count" the vertical and horizontal distances from one point to the other. The diagram shows going "down" 5 units (-5) and "right" 5 units (+5).
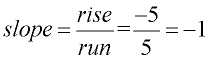
• Or you can use the formula. Let (-2,3) = ( x1, y1) and (3,-2) = ( x2, y2).
|
 |
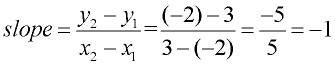
Slope at work in the real world:
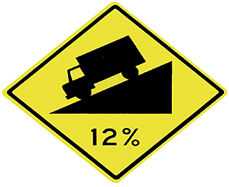
You have seen "slope at work" if you have seen a road sign indicating the steepness of a hill.
The sign, shown below, warns large vehicles that the road is about to decline at a grade of 12%. Such percentages are widely used in transportation to represent road inclines. A "grade of 12%" means a "slope of 0.12".
(Change the percentage to equivalent decimal form.)
A roadway displays the caution sign seen at the right. If the top of the hill is 360 vertical feet above the bottom of the hill, find the horizontal distance traveled as a truck goes straight down the hill from the top to the bottom. (Hint: Find the "run".)
|
 |
Interpreting Slope:
A variable that depends on another variable is called a dependent variable. For the equation y = 4x - 6, y is the dependent variable. The value of y depends upon the value chosen for x. It is often the case that the dependent variable is isolated on one side of the equation.
A variable in an equation that has its value chosen without restrictions imposed by another variable is called an independent variable. In the equation y = x - 6, x is the independent variable. |
Courtney remembers that her ATV had 4 gallons of gasoline in the tank on Monday. After driving a total of 40 miles during the week, she has 2 gallons of gas remaining.
• What is the slope of the graph representing Courtney's observations?
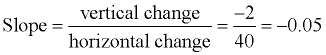
• What does the slope represent?
The slope represents the number of gallons of gas used per mile. The ATV is using 0.05 gallons of gasoline for every mile traveled. The negative value of the slope indicates that the amount of gas is decreasing.
• What is Courtney's overall miles per gallon based upon this information?
Courtney's overall miles per gallon is
20 miles on 1 gallon of gasoline (20 mpg). |
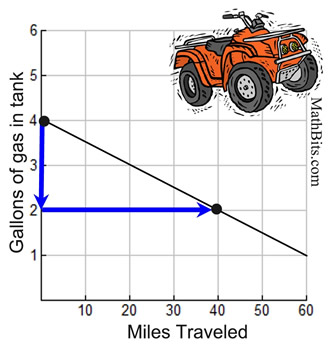
Notice that while we do not include unit labels on the statement of the slope, we do include unit labels on application problems based upon the conditions in the problem, such as 0.05 gallons per mile, or 20 miles per gallon. |
|
• Identify the dependent and independent variables in this problem.
The "Miles Traveled" is the independent variable and the "Gallons of Gas" is the dependent variable. The gallons of gas depends upon the number of miles traveled. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
