|
Like linear inequalities, quadratic inequalities may contain one variable or two variables.
While working with quadratic inequalities is, in many ways, similar to working with linear inequalities, the quadratic inequalities require a bit more thinking and testing. |

|
Solve the quadratic inequality x2 ≤ 4.
(one variable inequality) |
Let's think about this solution. If we change the inequality to an equal sign, we know that
x² = 4 has two possible solutions, 2 and -2. Now, the inequality states that we are looking for a squared value that is less than or equal to 4. Our first thought is that the answer will be less than or equal to 2. Good!
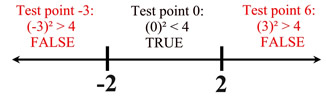
But, if we go too far in the negative direction, our answer will be wrong. Think about
x = -3. If we square -3 we get +9 which is not less than or equal to 4. We can only go in the negative direction until we hit -2. Our answers must be between -2 and 2, inclusive (including the -2 and the 2). |
Let's organize our thinking into steps:
1. Replace the inequality symbol with an equal sign, and solve the resulting equation. Solving the equation will give you numeric values that will form intervals that will reveal the solutions to the inequality.
2. Set up a number line to investigate the intervals created by the equation solutions. Pick a number in each interval and test it in the inequality. If the result is true, that interval is a solution to the inequality. There may be more than one interval which is a solution.
3. Graph the solution set. Since this is a "less than or equal to" inequality, closed circles are used to show that the endpoints are included in the solution. The shaded line segment indicates the other values for which the inequality is true. State the solution in a form directed by your teacher or stated in the question. |
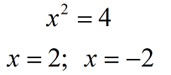

Ways to State the Solution:
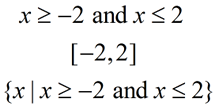
|

|
Solve the quadratic inequality x2 - 3x - 10 > 0.
(one variable inequality) |
Follow the same steps established in Example 1.
1.
Replace the inequality symbol with an equal sign, and solve the resulting equation. These solutions create the intervals that will reveal the solutions to the inequality.
2. Set up a number line to investigate the intervals created by the equation solutions. Pick a number in each interval and test it in the inequality. If the result is true, that interval is a solution to the inequality. There may be more than one interval which is a solution.
3. Graph the solution set. Since this is a "strict" inequality, open circles are used. Arrows indicate where the inequality is true. State the solution in a form directed by your teacher or stated in the question. |
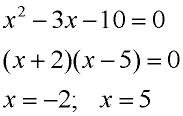


Ways to State the Solution:
x < -2 or x > 5
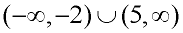
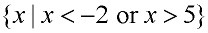
|


FYI: |
Graph the quadratic inequality y < x2 - 3x - 10.
(two variables inequality) |
1. Replace the inequality symbol with an equal sign, and graph the equation (a parabola). Use a dashed line for strict inequalities.
2. Choose a test point NOT on the parabola. Test the point in the inequality. If the result is true, shade the entire region where the test point lies. If the result is false, shade the entire region on the other side of the parabola. (The point (0,0) tests FALSE in the inequality.) 0 < 0² - 3(0) - 10 is false.
3. Solution: The shaded area contains all of the points that make the inequality true. |
|

|
How to use your
TI-83+ graphing calculator to graph quadratic inequalities.
Click calculator. |
|
|