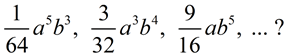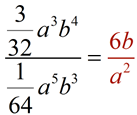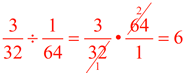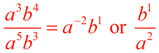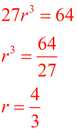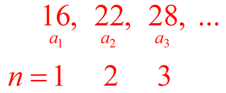| Find common difference or common ratio in a sequence. |
1) What is the common difference in the sequence
2m + 1, 4m + 4, 6m + 7, 8m + 10, ... ?
A "common difference" tells you that this is an arithmetic sequence where something is being added to each term to get the next term. To find what is being added, subtract any term from the term to its immediate right.
(4m + 4) - (2m + 1) = 2m + 3 is the common difference

2) What is the common ratio of the sequence
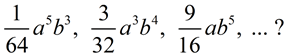
A "common ratio" tells you that this is a geometric sequence where something is being multiplied to each term to get the next term. To find what is being multiplied, divided any term by the term immediately in front (to the left) of it.
|
First, 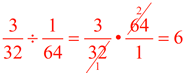
Now,
remember the rules for working with exponents involving division. Subtract the exponents, place result in numerator, or place where larger exponent resides. 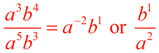
The common ratio is 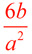 . .
|

3) What is the common ratio of a geometric sequence whose first term is 27 and whose fourth term is 64?
If the term numbers are small enough, make a visual of the sequence. 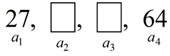
From the visual we can see that 27 • r • r • r = 64, or 27r3 = 64.
(27 gets multiplied by the common ratio 3 times to arrive at 64)
The common ratio is 4/3.
|
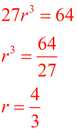
|
| Find a specific term in a sequence. |
1) Find the 12th term of the sequence an = n(n + 2).
Substitute the number of the term into the sequence formula.
a12 = 12 (12 + 2) = 12 (14) = 168

2) Find the 15th term of the sequence an = (-1)n-1n2.
Substitute the number of the term into the sequence formula.
a 15 = (-1)15-1152 = (-1)14152 = 1•225 = 225

3) Given { -3, 6, -12, 24, ... }, find the 15th term.
This is a geometric sequence. Each term is the previous term multiplied by (-2).
Using the format, an = a1 • r (n - 1), we know an = (-3)•(-2) (n - 1)
Now, substitute the number into the sequence formula.
a15 = (-3)•(-2) (15 - 1) = (-3)•(-2) (14) = -49152
| Analyze the problem and solve using sequence skills. |
1) The diagrams below represent the first three terms of a sequence, where the terms correspond to the number of shaded squares in each diagram.
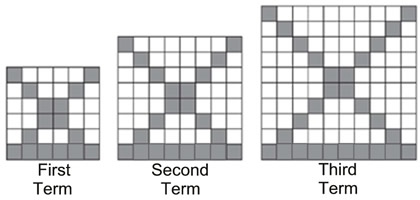
Assuming that this pattern continues, which formula determines an,
the number of shaded squares in the nth term?
1) an = 6n + 4 2) an = 6n + 8 3) an = 6n + 10 4) an = 6n + 12
Make a list of the shaded squares so you can see the developing pattern. |
First term has 16 shaded squares.
Second term has 22 shaded squares.
Third term has
28 shaded squares. |
16, 22, 28, ... represents the sequence.
The sequence is arithmetic
with a common difference of 6.
|
Examine the sequence as it relates to n: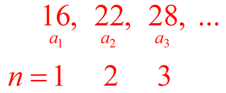 |
When n = 1, the term is 16 = 6•1 + 10.
When n = 2, the term is 22 = 6•2 + 10.
When n = 3, the term is 28 = 6•3 + 10.
Only choice 3 gives this pattern.
|

2) A seedling is 3 inches tall and is predicted to grow an additional 4 inches each week. Which of the following formulas can be used to predict the height of the seedling at the end of n weeks, assuming this growth pattern continues?
I. an = 4n + 3
II.
an = 3 + 4(n - 1)
III.
an = 4n - 1 |
 Working with "entities that are changing during a time period" can be tricky, such as working with "growth" or "decay". In relation to a time period, do you want to know the growth number at the START of a specific time period, or at the END of that time period?
Working with "entities that are changing during a time period" can be tricky, such as working with "growth" or "decay". In relation to a time period, do you want to know the growth number at the START of a specific time period, or at the END of that time period?
At the end of the first week, the seedling will be 7 inches tall. At the end of the second week it will be 11 inches tall and so on. Using a sequence to represent the height at the end of each week, we have 7, 11, 15, 19, ... (an arithmetic sequence). NOTE: You may be tempted to use 3 as the first term in the sequence, but you can think of 3 as not being the result of any growth period, so it not part of the sequence of growth.
Now, ...
Glance at the choices. By substitution of n = 1, 2, 3, 4, ...,
Choice I gives 7, 11, 15, 19, ...
Choice II gives 4, 11, 18, 25, ...
Choice III is a geometric sequence giving 1, 4, 16, 64, ...
Choices I represents the growth of the seedling.
See BEWARE: Sequences and Word Problems.

3) Given a sequence whose nth term is given by the explicit formula: an = 2n - 1
a) Write the first three terms of the sequence.
b) Find the 25th term.
c) Find the number of the term whose value is 407.
d) Will there be a term whose value is 90? Explain.
SOLUTION:
| a) Since n is a natural number (1, 2, 3, 4, ...), the first term of a sequence will begin with n = 1. |
| |
a1 = 2(1) - 1 = 1
a2 = 2(2) - 1 = 3
a3 = 2(3) - 1 = 5 |
Notice that n is replaced with the number of the term
you are trying to find. |
|
b) a25 = 2(25) - 1 = 49 |
c) 2n - 1 = 407
2n = 408
n = 204 The 204th term. |
d) No.
2n - 1 = 90
2n = 91
n = 45.5 (not a natural (counting) number)
You cannot have 45½ terms. The number of terms must be a counting number (1, 2, 3, ...).
|