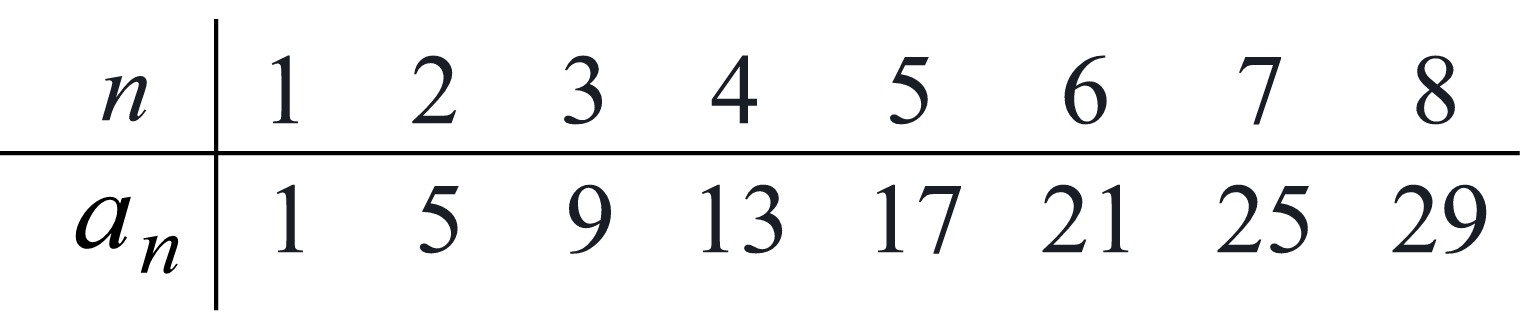|
 |
A sequence is an ordered list. It is a function whose domain is the natural numbers {1, 2, 3, 4, ...}. |
|
Sequence: |
1, |
5, |
9, |
13, |
17, |
21, |
... |
Notation for terms
of the sequence: |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
|
The three dots (...), called an ellipsis, at the end of the sequence, means that the sequence goes on forever (to infinity).
 Information about sequences:
• |
Each number in a sequence is called a term, an element or a member. |
• |
Terms of a sequence can be listed in set notation (curly braces): {1, 5, 9, 13, 17, 21, ...} |
• |
Terms are referenced in a subscripted form (indexed), where the natural number subscripts, {1, 2, 3, ...}, refer to the location (position) of the term in the sequence. The first term is denoted a1, the second term a2, and so on. The nth term is an.
|
• |
The terms in a sequence may, or may not, have a pattern or related formula.
Example: {1, 5, 9, 13, 17, 21, ...} can be generated by the formula an = 4n - 3.
Example: the digits of π form a sequence, but do not have a pattern. |
• |
Terms of the sequence are listed in a specific order. |
• |
A subscripted sequence is represented by a1, a2, a3, ... an, ... |
• |
Sequences are functions. |
• |
The domain of a sequence consists of the terms' location in the list, 1, 2, 3, 4, ... |
• |
The range of a sequence consists of the actual terms of the sequence. |
• |
When graphed, a sequence is a series of dots. (Do not connect the dots). |
• |
The sum of the terms of a sequence is called a series.
|
Forms of sequences:
• |
A finite sequence contains a finite number of terms (a limited number of terms) which can be counted.
Example: {1, 5, 9, 13, 17} (it starts and it stops)
Example: {5, 4, 3, 2, 1} (listing in descending order is possible)
Example: {m, a, n, d, y} (letters are possible. Sequence of letters in name "Mandy")
|
• |
An infinite sequence contains an infinite number of terms (terms continue without end) which cannot be counted.
Example: {1, 5, 9, 13, 17, 21, ...} (it starts but it does not stop, as indicated by the ellipsis ... )
Example: {15, 30, 45, 60, ...} (starting with any value is possible)
Example: {1, 2, 1, 2, 1, 2, ...} (a pattern of alternating order is possible)
Example: {a, b, c, a, b, c, ...} (letters are possible) |
Ways of expressing (or defining) sequences in Algebra 1:
• |
A sequence may appear as a list (finite or infinite):
Example: {1, 5, 9, 13, 17} finite
Example: {1, 5, 9, 13, 17, 21, ...} infinite
Listing makes it easy to see any pattern in the sequence. It will be the only option should the sequence have no pattern or formula. |
• |
A sequence may appear as an explicit formula. An explicit formula designates the nth term of the sequence, an , as an expression of n (where n = the term's location).
Example: {1, 5, 9, 13, 17, 21, ...} can be written in explicit form as an = 4n - 3.
(a formula in terms of n)
Read more at Sequences as Functions - Explicit |
Graphing Sequences:
Sequence: {1, 5, 9, 13, 17, 21, 25, 29, ...}
• Sequences are functions. They pass the vertical line test for functions.
• The domain consists of the term's location, the natural numbers, {1,2,3,...}, and the range consists of the actual terms of the sequence.
|
 |
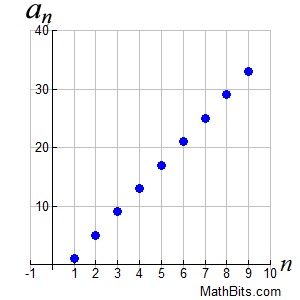• The graph will be in the first quadrant and/or the fourth quadrant (if sequence terms are negative).
• The graph will be a discrete graph (a series of dots) as you are graphing only specific points.
Do not connect the dots.
|
Some Sequences have Formulas:
Sequence: {1, 5, 9, 13, 17, 21, ...}
Term Number
|
Term |
Subscript Notation |
1 |
1 |
a1 |
2 |
5 |
a2 |
3 |
9 |
a3 |
4 |
13 |
a4 |
5 |
17 |
a5 |
6 |
21 |
a6 |
n |
|
an |
|
This sequence can be represented with a formula:
Formula: an= 4n - 3
Once a formula is known, you can quickly find ANY value in the sequence by using the term number and substitution.
To find the first term, let n = 1.
a1= 4(1) - 3 = 1
To find the second term, let n = 2.
a2= 4(2) - 3 = 5
To find the hundredth term, let n = 100.
a100= 4(100) - 3 = 397 |
Not all sequences can be expressed as a formula.
Special Types of Sequences:
There are several types of sequences (or even individual sequences) that are referred to by name.
Some of the more popular sequences are listed below.
• Arithmetic Sequences (such as {1, 5, 9, 13, 17, ...}
• Geometric Sequences (such as {2, 4, 8, 16, 32, ...}
• Quadratic Sequences (such as {4, 7, 12, 19, 28, ...}
• Harmonic Sequences (such as {-1, -1/2, -1/3, -1/4, ,,,}
• Triangular Number Sequence {1, 3, 6, 10, 15, 21, 28, ...}
• Fibonacci Sequence {0, 1, 1, 2, 3, 5, 8, 13 ,..}.
|
In Algebra 1, we will be concentrating on Arithmetic and Geometric Sequences.
Doubting Thomas wonders how we can know, for sure, that a sequence such as
{
2, 4, 6, 8, ...} is an arithmetic sequence. His theory is that there could be many other possible patterns, such as: 2, 4, 6, 8, 2, 4, 6, 8, ... (repeating 4 terms is his pattern).
|
Yes, Thomas is correct. Without a specification in the problem, there is the possibility of more than one pattern in most sequences. The person creating the sequence may have been thinking of a different pattern than what you see when you look at the sequence.
In Algebra 1, if in doubt, first look for arithmetic or geometric possibilities.
Math questions are usually not trying to trick you. |
 |
Note: The indexing (subscripts) used for sequences can technically begin with 0 or any positive integer. The most popular subscripting, however, begins with 1 so the subscript can also represent the position of the term in the sequence. Unless otherwise stated, this site will start subscripts at 1. |
|
Note: Computer programming languages such as C, C++ and Java, refer to the starting position in an array with a subscript of zero. Programmers must remember that a subscript of 3 refers to the 4th element, not the 3rd element, in the array. |
|
|
Arrow down to
"In Func MODE" |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
