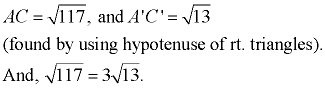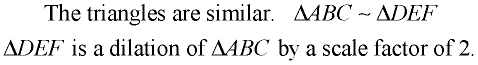|
|
Dilations are enlargements
(or reductions)!! |
|
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size.
• A dilation that creates a larger image is called an enlargement.
• A dilation that creates a smaller image is called a reduction.
• A dilation stretches or shrinks the original figure.
|
 |
• A description of a dilation includes the scale factor (or ratio) and the center of the dilation.
• The center of dilation is a fixed point in the plane.
•
If the scale factor is greater than 1, the image is an enlargement (a stretch).
• If the scale factor is between 0 and 1, the image is a reduction (a shrink).
• If the scale factor is 1, the figure and the image are congruent.
 |
The word "dilate" is often heard in relation to the human eye.
"The pupils of the eye were dilated."
As light hits the eye, the pupil enlarges or contracts
depending upon the amount of light.
|
Dilations can be seen, in a variety of situations:
Photography |
Arts and Crafts |
Graphing Calculator |
School or holiday picture packages offer the same photograph in a variety of sizes, from large to medium to small wallet size photos.
 |
Russian nesting dolls are a set of wooden dolls of decreasing size placed inside one another. After the smallest doll, each doll is an enlargement of its inside doll.
 |
The zoom feature will enlarge or reduce the viewing window.
 |
Food Service |
Logos |
Grow Toys |
Soft drink containers come in a variety of sizes. While some are of different shapes, others are simply enlargements.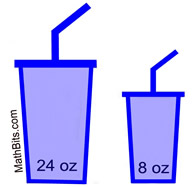 |
Product logos can come in a variety of sizes, such as these pizza shop logos on their small, medium and large boxes. |
Grow toys are sponge/foam toys that "grow" when placed in water. Some grow quickly, while others grow over several days. 
|
Dilations in the coordinate plane:
Most dilations in the coordinate plane use the origin, (0,0), as the center of the dilation.
 Dilation scale factor 2: Dilation scale factor 2:
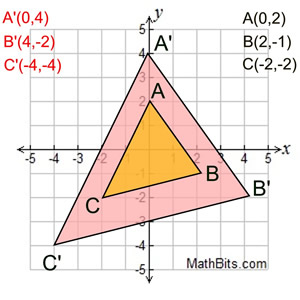 |
Starting with ΔABC, draw the dilation image of the triangle with a center at the origin and a scale factor of two.
Notice that every coordinate of the original triangle has been multiplied by the scale factor (x2).
Dilations involve multiplication!
Dilation with scale factor 2, multiply by 2.
(x, y) → (2x,2y) |
|
 Dilation scale factor ½:
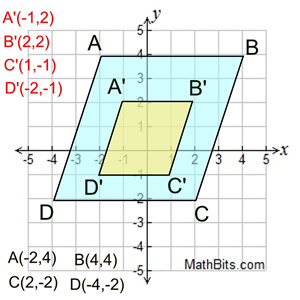 |
Starting with quadrilateral ABCD (blue), draw the dilation image of the quadrilateral with a center at the origin and a scale factor of ½.
Each vertex of ABCD is multiplied by ½.
Dilation with scale factor ½, multiply by ½.
(x, y) → (½x, ½y ) |
|
In this problem, the center of the dilation is NOT at the origin.
 Dilation not at origin:
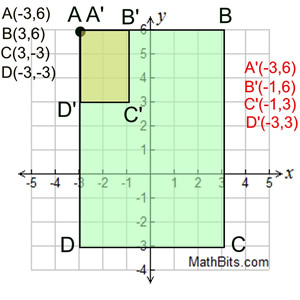 |
Starting with rectangle ABCD (green), draw the dilation image of the rectangle with the center of dilation at point A and a scale factor of 1/3
Notice that point A and its image are the same.
You must observe the distances from the center of the dilation at point A to the other points B, C and D. The dilation image will be 1/3 of each of these distances.
AB = 6, so A'B' = 2.
AD = 9, so A'D' = 3. Now, draw the image rectangle.
FYI:
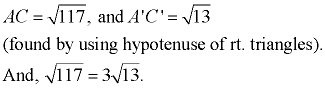
For a dilation not at the origin,
measure the distances. |
|
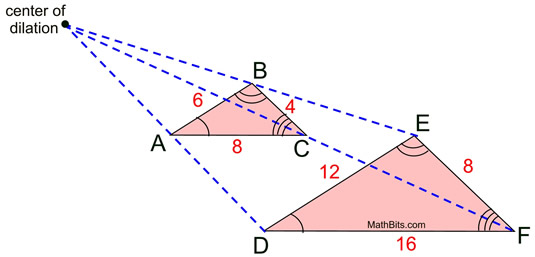
Dilations and Similarity:
The term similar (or similarity) can be defined using the language of transformations.
|
Two figures are similar if one is the image of the other under a transformation from the plane into itself that multiplies all distances by the same positive scale factor. That is to say, one figure
is a dilation of the other. |
|
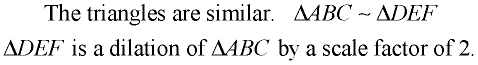


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|