Continuous and Discrete Functions MathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

From working with statistics, we know that data can be numerical (quantitative) or descriptive (qualitative). When data is numerical, it can also be discrete or continuous.

Let's take a look at a comparison of these concepts:

Continuous	Discrete
Definition: A set of data is said to be continuous if the values belonging to the set can take on ANY value within a finite or infinite interval.	Definition: A set of data is said to be discrete if the values belonging to the set are distinct and separate (unconnected values).
Examples: • The height of a horse (could be any value within the range of horse heights). • Time to complete a task (which could be measured to fractions of seconds). • The outdoor temperature at noon (any value within possible temperatures ranges.) • The speed of a car on Route 3 (assuming legal speed limits).	Examples: • The number of people in your class (no fractional parts of a person). • The number of TV sets in a home (no fractional parts of a TV set). • The number of puppies in a liter (no fractional puppies). • The number of questions on a math test (no incomplete questions).
NOTE: Continuous data usually requires a measuring device. (Ruler, stop watch, thermometer, speedometer, etc.)	NOTE: Discrete data is counted. The description of the task is usually preceded by the words "number of...".
Function: In the graph of a continuous function, the points are connected with a continuous line, since every point has meaning to the original problem.	Function: In the graph of a discrete function, only separate, distinct points are plotted, and only these points have meaning to the original problem.
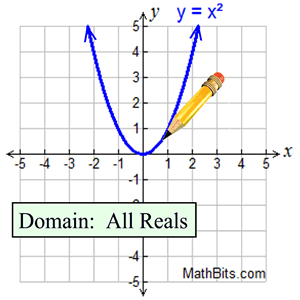
Graph: You can draw a continuous function without lifting your pencil from your paper.	Graph: A discrete graph is a series of unconnected points (a scatter plot).
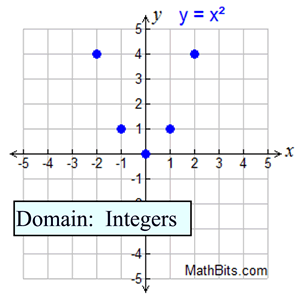
Domain: a set of input values consisting of all numbers in an interval.	Domain: a set of input values consisting of only certain numbers in an interval.
In Plain English: A continuous function allows the x-values to be ANY points in the interval, including fractions, decimals, and irrational values.	In Plain English: A discrete function allows the x-values to be only certain points in the interval, usually only integers or whole numbers.
Why do we care? When graphing a function, especially one related to a real-world situation, it is important to choose an appropriate domain (x-values) for the graph. For example, if a function represents the number of people left on an island at the end of each week in the Survivor Game, an appropriate domain would be positive integers. Hopefully, half of a person is not an appropriate answer for any of the weeks. The graph of the people remaining on the island would be a discrete graph, not a continuous graph.

For help with continuous and discrete functions on your calculator, Click Here!