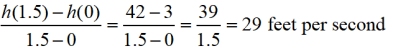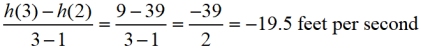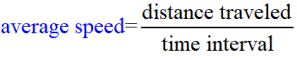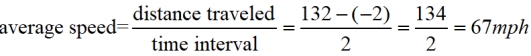|
 Linear Functions: You are already familiar with the concept of "average rate of change".
When working with straight lines (linear functions) you saw the "average rate of change" to be:
The word "slope" may also be referred to as "gradient", "incline" or "pitch", and be expressed as:

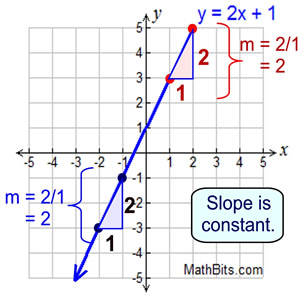
A special circumstance exists when working with straight lines (linear functions), in that the "average rate of change" (the slope) is constant. No matter where you check the slope on a straight line, you will get the same answer.
|
|
 Non-Linear Functions: Non-Linear Functions:
When working with non-linear functions, the "average rate of change" is not constant.
The process of computing the "average rate of change", however, remains the same as was used with straight lines: two points are chosen, and 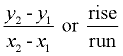 is computed. is computed.
FYI: You will learn in later courses that the "average rate of change" in non-linear functions is actually the slope of the secant line passing through the two chosen points. A secant line cuts a graph in two points. |
|
 When you find the "average rate of change" you are finding the rate at which (how fast) the function's y-values (output) are changing as compared to the function's x-values (input). When you find the "average rate of change" you are finding the rate at which (how fast) the function's y-values (output) are changing as compared to the function's x-values (input).
When working with functions (of all types), the "average rate of change"
is expressed using function notation.
Average Rate of Change
For the function y = f (x) between x = a and x = b, the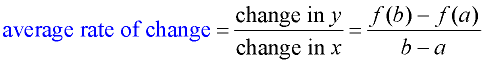
|
While this new formula may look strange, it is really just a re-write of 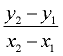 . .
Remember that y = f (x).
So, when working with points (x1, y1) and (x2, y2), we can also write them as
the points 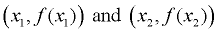 . .
Then our slope formula can be expressed as 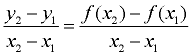 . .
If we rename x1 to be a, and x2 to be b, we will have the new formula.
The points are 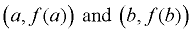 , and the , and the
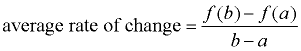 . .
(Just remember that it is the "slope" formula.)

 Finding average rate of change from a table. Finding average rate of change from a table.
Function f (x) is shown in the table at the right.
Find the average rate of change over the interval 1 < x < 3.
Solution:
If the interval is 1 < x < 3, then you are examining the points from (1,4) to (3,16). From the first point, let a = 1, and f ( a) = 4. From the second point, let b = 3 and f ( b) = 16.
Substitute into the formula:
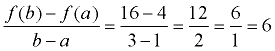
|
|
The average rate of change is 6 over 1, or just 6 over the interval 1 < x < 3.
The y-values change 6 units every time the x-values change 1 unit, on this interval. |
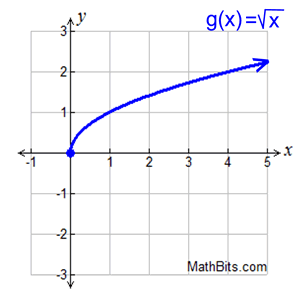
 Finding average rate of change from a graph. Finding average rate of change from a graph.
Function g (x) is shown in the graph at the right.
Find the average rate of change over the interval
1 < x < 4.
Solution:
If the interval is 1 < x < 4, then you are examining the points (1,1) and (4,2), as seen on the graph. From the first point, let a = 1, and g ( a) = 1. From the second point, let b = 4 and g ( b) = 2.
Substitute into the formula: 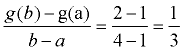
|
|
The average rate of change is 1 over 3, or just 1/3 on the interval 1 < x < 4.
The y-values change 1 unit every time the x-values change 3 units, on this interval. |
 Finding average rate of change from a word problem. Finding average rate of change from a word problem.
A ball thrown in the air has a height of h(t) = - 16t² + 50t + 3 feet
after t seconds.
a) What are the units of measurement for the average rate of change
of h?
b) Find the average rate of change of h between t = 0 and t = 1.5.
c) Find the average rate of change of h between t = 2 and t = 3.
|
|
Solution:
a) In the formula, 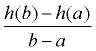 , the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.
b) Start by finding h( t) when t = 0 and t = 1.5, by plugging the t values into h(t).
|

In Example 3, we saw a rate of change problem whose results
carried with them (+) or (-) signs to designate
the direction of the ball (rising versus falling).
Due to this designation of "direction",
the answers are referred to as velocity and not speed.
Unlike velocity, speed is always positive.
Speed is the ratio of the distance traveled to the time interval.
(Distance is always positive. Time is a always positive. Speed is a always positive.)
| Think about a car speedometer.
The speedometer tells you the car's speed
in miles per hour,
and the result is always a positive number.
The speedometer does not register
negative
numbers when the car backs up.
Speed does not care about "direction".
|
 |

When dealing with "average rate of change",
you may encounter questions that ask you to find the "average speed".
Average Speed
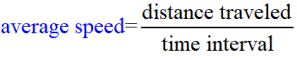
|
Caution: Remember, speed is always positive. Speed does not indicate direction (it is not a vector).
If direction is involved, you are dealing with velocity - which is speed with a direction (displacement).
(The difference between speed and velocity will be a big deal when you take Physics.)
 Finding average speed from a word problem. Finding average speed from a word problem.
A car's starting position on a number line (representing "miles"), is located at -2. At the end of a trip, the car's position is at 132 on the number line. The trip takes 2 hours.
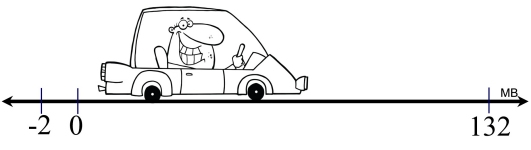
What is the average speed of the car during this trip?
|
Solution:
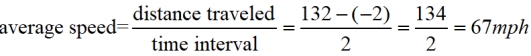 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

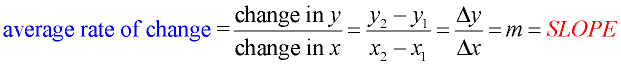

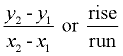 is computed.
is computed.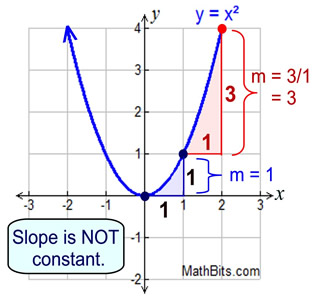
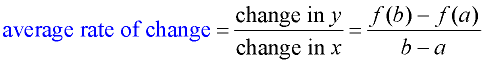
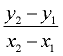 .
.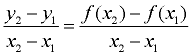 .
.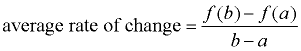 .
.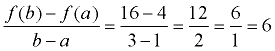
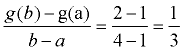

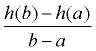 , the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.
, the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the ball.