|
This is a unique factoring method for trinomials
of the form ax2 + bx + c where a ≠ 1.
(This "ac" Method is a slight variation of a similar method referred to as "Slide and Divide", or "Slip and Slide".)
While this method is interesting to investigate, you should not rely on it as your only method of factoring trinomials with a coefficient other than one. Unique (strange) methods, such as this, can be easily forgotten. Be sure you understand methods that are based on logical process rather than ones based more upon memorization. You are more likely to remember a logical process.
 The "ac" Method of Factoring Trinomials with a ≠ 1 |
Factor: 3x2 + 13x - 10
|
1: Since this method is referred to as "ac", we start with a, the leading coefficient and c, the constant.
Replace the constant with a times c.
Remove the leading coefficient.
This new trinomial is no longer equivalent to the original trinomial. What's going on here? |
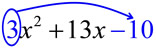x2 + 13x - 30 |
2: The new trinomial can be factored easily. |
(x + 15)(x - 2)
|
3: Replace x with the original leading coefficient times x. The original leading coefficient was 3. |
(3x + 15)(3x - 2) |
4: One of the factors can now be factored further. |
3(x + 5)(3x - 2) |
5: Divide by the original leading coefficient (which was 3), and you will have the final factored form. |
(x + 5)(3x - 2) Ans. |
 |
Now, honestly ...
do you really think you will remember all of these "weird" steps next year, when you
need to factor? |
While this may not be a factoring method of choice, this method is worthy of an investigation into its validity. How can these seemingly random changes to and from non-equivalent forms result in a correct answer?
When we break this process down and attempt to validate each of the steps, we discover that there is more going on here than we are led to believe. The description of the "ac" method is simply a shorthand version of the actual process and is mathematically confusing.
| Here is the entire process and its rationale. |
1. 3(3x2 + 13x - 10) |
1. The original expression is multiplied times the leading coefficient. (Multiplication) |
2. 9x2 + 39x - 30 |
2. Distributive Property |
3. (3x)2 + (3x)13 - 30 |
3. Factor first two terms. |
4. (p)2 + (p)13 - 30 = p2 + 13p - 30 |
4. Replace (3x) with another variable, such as p. Let 3x = p. Substitution. |
5. (p + 15)(p - 2) |
5. Factor. |
6. (3x + 15)(3x - 2) |
6. Replace p with 3x. Substitution. |
7. 3(x + 5)(3x - 2) |
7. Factor further. |
8. 3(3x2 + 13x - 10) = 3(x + 5)(3x - 2) |
8. This expression is still equivalent to the expression in step 1. |
9. (3x2 + 13x - 10) = (x + 5)(3x - 2) |
9. Divide both sides by 3, which will undo the initial process of multiplying by 3. The result is now equivalent to the original expression and is the answer. |
While this entire process starts by multiplying by the leading coefficient, all other steps keep the expressions equivalent to the expression in step 1 (which is 3 times the original expression). When the process is finished, the expression is divided by 3 (the leading coefficient), which makes the answer equivalent to the original expression. Thus, it is a valid process.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
