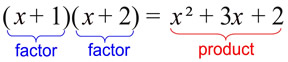|
When you are asked to "factor" an expression,
you are being asked
to write the expression as the product (multiplication) of other expressions.
|
You can think of factoring as playing the game-show "Jeopardy" where you are shown an answer and asked to find the question. In factoring, you are given the answer to a multiplication, and asked to find the numbers or expressions that were multiplied to get this answer.
At times, finding factors can be a challenge! But don't panic! The more factoring problems you see, the more strategies you will acquire and the easier "the game" will become. So, get those spidey senses ready.
|
 |
A factor is a number (or algebraic expression) that divides another number (or expression) evenly, with no remainder. |
In other words, factors (plural) are numbers that can be multiplied to form another number.
Factors are usually positive or negative integers. |
|
When two numbers (or expressions) are multiplied, the answer is called a product.
The numbers (or expressions)
that are multiplied to form the product are called factors.
|
Numeric Example:
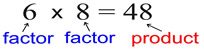 |
Algebraic Example:
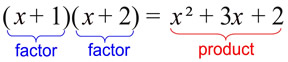 |
To factor (also called factoring or factorizing) is the process of finding the factors.
The factored form on an expression is equivalent to the original expression.
 |
| When considering the lists of factors of two integers, a common factor is any factor that is shared by (found in) both of the lists of factors. |
Consider the factors of 18 and 24.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors are 1, 2, 3, 6.
(1, 2, 3 and 6 appear in both lists of factors)
|
|
Consider: (18 + 24) could be factored as
• 2(9 + 12)
• 3(6 + 8)
• 6(3 + 4)
All of these combinations are
possible "factorings" of (18 + 24). |
|
While there may be numerous common factors, there is only one of the factors that is the greatest common factor (GCF). In this example, the GCF = 6.
When factoring out the GCF, the remaining
expression cannot be further factored by another common factor.
6(3 + 4) = 6(3 + 4) done!
2(9 + 12) = 2(3(3 + 4)) = 6(3 + 4)
3(6 + 8) = 3(2(3 + 4)) = 6(3 + 4)
|
When you are asked to factor an expression in Algebra, it is understood that you are being asked to factor completely. Your final answer should not need any further factoring.
So, when you are asked to factor an expression, start by finding the greatest common factor.
This method will save you additional work, and arrive at the answer more quickly. |

 The first step in a factoring problem is to find, The first step in a factoring problem is to find,
and then factor out, the greatest common factor. |
Let's look at "finding" the GCF:
|
Find the greatest common factor of
12, 24, and 42. |
Solution:
|
Factors of 12: 2,3,4,6,12
Factors of 24: 2,3,4,6,8,12,24
Factors of 42: 2,3,6,7,21,42
Greatest Common Factor = 6 |
| |
|
|
Find the GCF of the terms x3, x2 and x5. |
Solution: |
The highest power of x that is common to all three of the terms is x2.
Greatest Common Factor = x2. |
| |
|
|
Find the GCF of the terms 3a3b4, 6a4b2, and 12a6b. |
Solution: |
The highest power of a that is common to all three of the terms is a3.
The highest power of b that is common to all three of the terms is b.
The GCF of the coefficients 3, 6 and 12, is 3.
Greatest Common Factor = 3a3b. |
|
|
 |
Find the GCF of the following terms:
3(x + 1)3, 9(x + 1)2, and 12(x + 1). |
| Solution: |
The GCF of 3, 9 and 12 is 3.
The highest power of the expression (x + 1) is (x + 1)1.
Greatest Common Factor = 3(x + 1). |
To see "finding" and "factoring out" the GCF in polynomials go to
Greatest Common Factor and Polynomials.

|
For help with factoring on your calculator,
Click Here!
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|