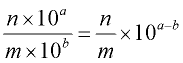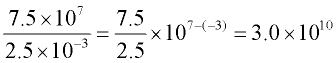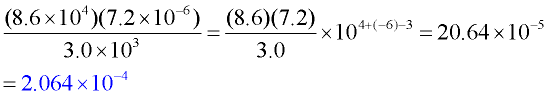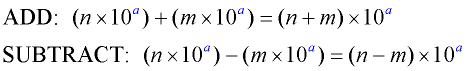|
Scientific notation is a shorthand method of expressing very large or very small numbers. Calculators, scientists and engineers find this base 10 method of expressing values to be very helpful, as it allows for very precise calculations.
While there are many ways to write values to a power of 10, there is only one format that is accepted as proper "scientific notation".
 Proper Scientific Notation:
To convert to scientific notation:
• The value is rewritten to contain a decimal point with ONE non-zero digit to the left of the decimal point.
• This result is then multiplied by a power of 10, where the exponent represents the number of moves necessary to return the value to its original state.
• If the decimal must move to the right, the exponent is positive. If the decimal must move to the left, the exponent is negative.
|
 Note: Since we are dealing with | a |, the a could be either positive (3×105) or
negative (-3×105). |
Proper notation:
5.3 x 1024 is proper scientific notation.
74.2 x 10-15 is not proper scientific notation because there are 2 digits preceeding the decimal point.
|
Converting to Scientific Notation: |
1. Given: 52,400,000
Start by rewritting the number so only one digit is to the left of the decimal point, which will be 5.24.
Now, for that value to be equivalent to 52,400,000 the decimal must move 7 places to the right, telling us the needed exponent is 7.
|
ANSWER: 5.24 x 107 |
2. Given: 0.000012
Start with 1.2. Now, the decimal point needs to move 5 places to the left to get 0.000012, so the exponent is -5. |
ANSWER: 1.2 x 10-5 |
3. Express the speed of light (300,000,000 m/sec) in scientific notation.
Start with 3.0. Now the decimal needs to move 8 places to the right to get 300,000,000, so the exponent is 8. |
ANSWER: 3.0 x 108 m/sec |
Converting from Scientific Notation:
We will be referring to values written as numerals (regular numbers) as "standard notation". |
1. Given: 3.805 x 105
This number is in scientific notation. The positive exponent indicates that a movement of the decimal point 5 places to the right will show the value in standard (regular number) form. |
ANSWER: 380,500 |
2. Given: 6.5 x 10-6
This number is in scientific notation. The negative exponent indicates that a movement of the decimal point 6 places to the left will show the standard form. |
ANSWER: 0.0000065 |
3. Express the half-life of Plutonium (8.0 x 107years) in standard notation.
This number is in scientific notation. The positive exponent indicates that a movement of the decimal point 7 places to the right will show the standard form. |
ANSWER: 80,000,000 yrs. |
REAL WORLD ACCURACY: The multiplication (or division) of values expressed in scientific notation may result in answers with "more decimal accurray" than the original values. In real world situations, the multiplication (or division) of values cannot result in answers with a higher level of accuracy than the original values. In fact, the answer cannot be stated to any higher level of accuacy than the number of digits in the least accurate number.
For example, in Example 3 above, the answer is 2.064 x 10-4. Had this been a real-world problem, the accuracy of the answer would not exceed the least accurate listings in the problem of one decimal place. The real-world answer would be 2.1 x 10-4.
|
Adding and Subtracting Scientific Notation: |
To ADD or SUBTRACT two numbers in scientific notation, the exponents on the power of 10 must be the same. You may need to "adjust" the numbers, moving them out of scientific notation, so the exponents are alike.
|
|
|
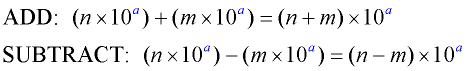
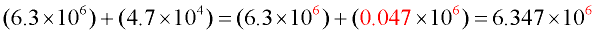
The decimal point in the second number was moved two places to the left so that the base of 10 could be raised to a power of 6. |
Scientific Notation on the Calculator:
Check to see if your calculator offers a SCI mode (for answers to be expressed in scientific notation). Also, remember that calculators can accept the ^ symbol as an indication of exponent. For example, 5 3 can be entered as 5 ^ 3. The * signifies x (multiplication).
|
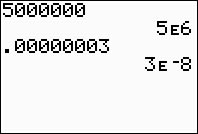In SCI mode, answers are
displayed in the calculator's
scientific notation format.
5E6 = 5 x 106
|
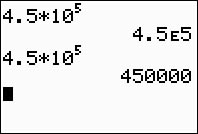First entry: SCI mode
Second entry: NORMAL mode
|
|
For help with scientific notation on your calculator,
click here. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
