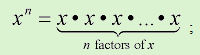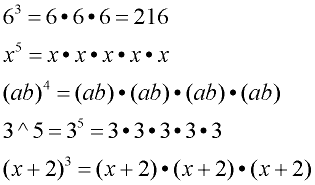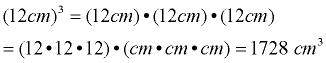Exponents represent mathematical shorthand for multiplication.
Numbers expressed using exponents are called "powers".
Older calculators and computers often use the operator ^ to represent an exponent.

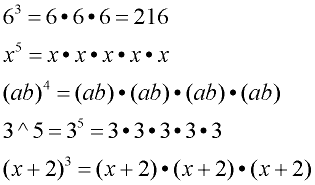
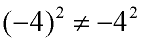To apply an exponent to a base value which is negative, the base value must be enclosed in a set of parentheses: (-4)2 = (-4) • (-4) = 16. The exponent then applies to the entire set of parentheses to which it is attached. But, if the base value is not enclosed in parentheses, the exponent applies only to the number to which it is attached. It does not apply to the negative sign:   -42 = -(4) • (4) = -16. Think of the negative sign as a multiple of (-1):    -42 = (-1) • (42 ) = (-1) • (4) • (4) = -16. or as the "opposite" of 42. (-4)2 is "negative 4 quantity squared".   -42 is "negative of 4 squared" or "opposite of 42 ".

Naming:  2⁴ is read "two raised to the 4th power" or just "two to the 4th".

Exponents of 2 and 3 have specific designations:  
2² is read "two squared" and 2³ is read "two cubed".

Units:  When applying an exponent to a value with labeled units, be sure to also apply the exponent to the units:	For help with exponents on your calculator, click here.

Exponent of 1: A value raised to an exponent of "one" is equal to itself.
The exponent of one states the number of times the base is multiplied by itself. Since the base is the only factor (occurs once) in the multiplication, it equals itself.